Карло Ровелли - Нереальная реальность. Путешествие по квантовой петле

Это первый математический закон, открытый для земных предметов: закон падения тел [37]. До этого момента были открыты лишь математические законы движения планет. Математическое совершенство больше не ограничено небесами.

И все же величайший результат еще впереди, и получит его не кто иной, как Исаак Ньютон. Ньютон тщательно изучает результаты Галилея и Кеплера и, объединяя их, находит настоящий скрытый бриллиант. Мы можем проследить за его рассуждениями на примере «маленькой луны», как делает он сам в «Математических началах натуральной философии» – книге, в которой оформились основания современной науки.

Представьте себе, что Земля, пишет Ньютон, имеет много лун, подобно Юпитеру. Помимо настоящей Луны, вообразим другие спутники, и в частности маленькую луну, которая обращается вокруг Земли на минимальном расстоянии от нее, чуть выше горных пиков. С какой скоростью двигалась бы эта маленькая луна? Один из открытых Кеплером законов связывает радиус орбиты с периодом обращения, то есть с временем, которое уходит на один полный оборот [38]. Мы знаем радиус орбиты настоящей Луны (Гиппарх измерил его еще в древности) и ее период обращения (один месяц). Мы знаем радиус орбиты маленькой луны (радиус Земли измерен Эратосфеном в древности). Из простой пропорции можно вычислить орбитальный период маленькой луны. Получается полтора часа. Маленькая луна совершала бы один оборот вокруг Земли каждые 90 минут.

Далее, находящийся на орбите объект не движется прямолинейно: он постоянно изменяет направление, а изменение направления – это ускорение . Маленькая луна ускоряется в направлении центра Земли. Это ускорение нетрудно подсчитать [39]. Ньютон делает простые вычисления и в результате получает… 9,8 метра в секунду за секунду! То же самое ускорение, что и у Галилея в экспериментах с падающими телами на Земле.

Совпадение? Не может быть, заключает Ньютон. Если результат одинаков – ускорение вниз величиной 9,8 метра в секунду за секунду, – то и причина должна быть одна. А значит, сила, которая заставляет маленькую луну обращаться по своей орбите, должна быть той же, что заставляет предметы падать на земную поверхность .

Мы называем силу, заставляющую предметы падать, гравитацией. Ньютон понимает, что эта самая гравитация заставляет маленькую луну обращаться вокруг Земли. Без гравитации она улетела бы прочь по прямолинейной траектории. Но тогда и настоящая Луна тоже должна обращаться вокруг Земли из-за гравитации! И спутники Юпитера притягиваются Юпитером, и планеты, которые обращаются вокруг Солнца, притягиваются Солнцем! Без этого притяжения любое небесное тело двигалась бы прямолинейно. И тогда Вселенная – это огромное пространство, где тела притягиваются друг к другу определенными силами и существует универсальная сила гравитации: каждое тело притягивается ко всем другим телам.

Грандиозная картина обретает форму. Внезапно, спустя тысячелетие исчезает разделение между небесами и Землей: больше нет «естественного уровня» для вещей, как предполагал Аристотель, нет центра мира, предметы обретают свободу и больше не стремятся к своему естественному месту, но движутся прямолинейно и вечно.

Простой расчет с маленькой луной позволяет Ньютону вывести, как гравитация меняется с расстоянием, и определить ее силу [40], характеризуемую величиной, которую сегодня называют ньютоновской гравитационной постоянной и обозначают буквой G (от слова gravity ). На Земле эта сила заставляет предметы падать, в небесах она удерживает планеты и спутники на своих орбитах. Но это одна и та же сила.

Это – крушение аристотелевской картины мира, которая доминировала в представлениях людей на протяжении Средних веков. Подумайте, например, о вселенной Данте: как и у Аристотеля, Земля – это шар в центре Вселенной, окруженный небесными сферами. Теперь это не так. Вселенная – это громадное, бесконечное пространство, усеянное звездами, без границ и без какого-либо центра. Материальные тела в ней движутся свободно и прямолинейно, если только сила, порожденная другими телами, не отклоняет их. Отсылки к античному атомизму хорошо видны у Ньютона, даже когда он использует общепринятые понятия:

Мне кажется вероятным, что Бог вначале дал материи форму твердых, массивных, непроницаемых, подвижных частиц таких размеров и фигур и с такими свойствами и пропорциями в отношении к пространству… [41]

Мир ньютоновской механики прост и представлен на рис. 2.1 и 2.2. Это – возрожденный мир Демокрита. Мир, состоящий из огромного однородного пространства, всегда и везде подобного самому себе, в котором частицы вечно движутся, взаимодействуя друг с другом, – и ничего больше. Мир, воспетый Леопарди:

Рис. 2.1.Из чего состоит мир?

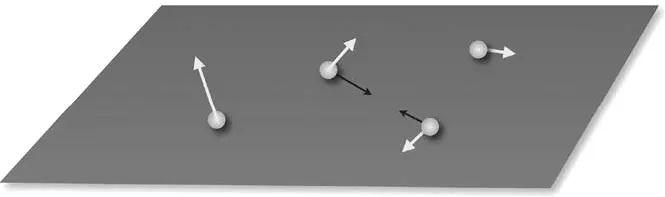
Рис. 2.2.Мир Ньютона: частицы, которые с течением времени движутся в пространстве, притягиваемые силами

Но эта картина намного сильнее демокритовского представления, поскольку это не просто мысленный образ, с помощью которого упорядочивается мир. Теперь эта картина объединена с математикой – наследием Пифагора и великой традицией математической физики александрийских астрономов. Мир Ньютона – это мир Демокрита, выраженный математическими средствами.

Ньютон без всяких колебаний признает, что новая наука очень многим обязана науке античной. Например, в первых же строках своего «Трактата о системе мира» [43]он указывает (корректно) на античное происхождение идеи, лежащей в основе коперниканской революции: «По мнению древних философов, в высочайших частях мира звезды закреплены и находятся в неподвижности, а Земля обращается вокруг Солнца»; однако он немного ошибается относительно достижений и открытий ученых прошлого и цитирует – иногда к месту, иногда нет – Филолая, Аристарха Самосского, Анаксимандра, Платона, Анаксагора, Демокрита и (!) «ученого Нума Помпилия, царя римлян».

Сила новой ньютоновской интеллектуальной парадигмы превзошла самые смелые ожидания. Вся технология XIX века и нашего современного мира основывается по большей части на ньютоновских формулах. Прошло три столетия, но мы по-прежнему сооружаем мосты, поезда и небоскребы, двигатели и гидравлические системы благодаря теориям, строящимся на ньютоновских уравнениях. Благодаря Ньютону мы знаем, как управлять самолетом, как делать метеорологические прогнозы, как предсказывать существование еще не обнаруженных планет и как отправлять космические аппараты на Марс… Современный мир не родился бы без маленькой луны Ньютона.