Георгий Гамов - Мистер Томпкинс внутри самого себя

Задолго до того, как Юнг проделал свой эксперимент, сэр Исаак Ньютон обнаружил, что если белый свет пропустить через стеклянную призму, то под различными углами получится свет различного цвета.

Если за призмой поставить экран, то на нем мы увидим то, что принято называть спектром. Белый свет, заключил Ньютон, — это смесь различных цветов; каждый из цветов при прохождении сквозь призму отклоняется под определенным углом. Именно так возникает радуга в небе, когда солнечный свет преломляется и отражается, проходя сквозь взвешенные в воздухе капельки воды.

После того, как Юнг произвел свой эксперимент с интерференцией света, стало ясно, что спектр можно получить и без призмы. Достаточно взять стеклянную или металлическую поверхность и нанести на нее очень тонкие прямые линии через правильные интервалы, длина которых сравнима с длиной волны света. Такая разлинованная поверхность называется решеткой. Затем вы направляете на такую решетку под некоторым углом пучок света. Для простоты предположим, что свет монохроматический, т.е. состоит из волн одной длины, или имеет только один цвет. Когда свет падает на решетку, каждая точка между линиями действует как источник света. Если теперь мы воспользуемся линзой, чтобы образовать на экране изображение решетки, то на экране найдется точка, расстояния от которой до точек на решетке отличаются на целое число длин волн. Это означает, что гребни волн, приходящих от этих точек, усиливают друг друга, и мы получаем на экране яркое пятно. Разумеется, положение этого пятна зависит от длины волны света. Свет с другими длинами волн (других цветов) будет образовывать яркие пятна в других местах экрана, поэтому белый свет разложится в спектр, как при прохождении сквозь призму.

Зная угол отражения и расстояние между линиями решетки, мы легко можем определить длину волны света любого цвета. Именно так и была определена длина волны света. Голубой свет имеет длину волны около четырех стотысячных сантиметра, красный — примерно вдвое большую длину волны.

— Очень короткие волны по сравнению с радиоволнами, — счел нужным заметить мистер Томпкинс.

— А длины волн рентгеновского излучения еще гораздо короче, — подтвердил доктор Экскинс. — Когда немецкий физик Рентген в 1895 году открыл икс-лучи, природа загадочного излучения не была известна. Впоследствии было установлено, что оно в известной мере аналогично свету, но имеет намного более короткую длину волны. Чтобы доказать, что рентгеновское излучение аналогично свету, было необходимо продемонстрировать какое-нибудь интерференционое явление. Но если рентгеновское излучение имеет по сравнению со светом гораздо более короткую длину волны, то и линии на решетке должны располагаться гораздо теснее — намного ближе друг к другу, чем можно было изготовить. Возникло весьма затруднительное положение.

В 1912 году этой проблемой занялся немецкий физик Макс фон Лауэ. Из беседы с двумя другими учеными он узнал, что атомы в кристаллах расположены с удивительной правильностью на расстоянии примерно 10~8 см друг от друга, и понял, что кристалл — идеальная решетка, созданная самой природой!

Спешно вернувшись в свою лабораторию, фон Лауэ пропустил пучок рентгеновских лучей через кристалл сульфида цинка и обнаружил на фотопластинке, игравшей роль экрана, красивый узор из светлых пятен. Проблема была решена! Рентгеновское излучение действительно вело себя, как световые волны, только длина волны была намного короче. Что же касается длины волны рентгеновского излучения, то она была известна из других работ, равно как и расстояние между атомами. Оказалось, что длина волны рентгеновского излучения примерно в тысячу раз короче, чем у видимого света, и сравнима с расстоянием между атомами в кристалле.

Но коль скоро межатомные расстояния и длина волны рентгеновского излучения известны, задачу можно обратить: по расстояниям между светлыми пятнами на фотопластинке в принципе можно, рассуждая «обратным ходом», восстановить расположение атомов в кристалле неизвестной структуры. Именно так мы и узнаем структуру сложных белков и других больших молекул живой материи.

— А как вы решаете задачу «обратным ходом»? — поинтересовался мистер Томпкинс. — Английский физик сэр Уильям Генри Брэгг первым обратил внимание на то, что кристаллы в атомах проще всего рассматривать как расположенные плоскостями, вроде параллельных бумажных листов на некотором расстоянии друг от друга. В сечении это выглядит вот так.

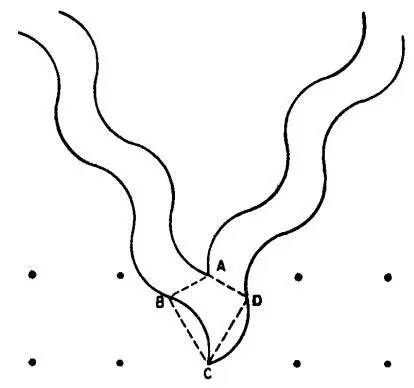
Отражение рентгеновских лучей в кристалле Доктор

Экскинс набросал на доске схему.

— Рентгеновское излучение отражается от плоскостей так же, как свет от зеркал. Если две вереницы, или, как принято говорить, два цуга рентгеновских волн распространяются в одной фазе, гребень к гребню, впадина к впадине, то после отражения волны уже не будут идти в таком согласии по той простой причине, что нижней волне необходимо преодолеть дополнительное расстояние BCD, и она отстанет. Но если на участке и BCD укладывается ровно одна длина волны, то после отражения волны по-прежнему будут распространяться в одной фазе, так как гребень нижней волны будет идти «нога в ногу» с гребнем верхней волны. То же самое произойдет и в том случае, если на участке BCD укладывается 2, 3, 4 или любое другое целое число длин волн. Если вы хотя бы немного помните тригонометрию, то для вас не составит труда вывести знаменитую формулу Брэгга, которая утверждает, что гребни и впадины волны будут идти «нога в ногу», если λ = 2d sin α, или 2λ = Id sin α, или Зλ = 2d sin α, а в общем виде — если nλ = 2d sin α, где п — произвольное целое положительное число, λ — длина волны рентгеновского излучения, d — расстояние между плоскостями в кристалле и α — угол отражения.

— А что, собственно говоря, означает формула Брэгга? — спросил мистер Томпкинс, который был не очень силен в тригонометрии.

— Она означает, что плоскости в кристалле нельзя считать зеркалами в обычном смысле, так как отражение от них происходит только под определенным углом. По другим направлениям между волнами происходит так называемая разрушительная интерференция. Попросту говоря, они гасят друг друга. Красота формулы Брэгга заключается в том, что если известны длина волны рентгеновского излучения А и угол отражения а, то с ее помощью можно найти расстояние d между плоскостями. Правда, необходимо также знать число п, т.е. сколько длин волн укладывается в дополнительном отрезке пути, но я не хочу обременять вас излишними подробностями.

— Блестяще! — с восхищением заметил мистер Томпкинс. — А что произойдет, если атомы в кристалле расположатся в виде плоскостей не совсем точно?