Лоуренс Краусс - Почему мы существуем? Величайшая из когда-либо рассказанных историй

Если мы добавим к этой комбинации еще одну волну с немного другой длиной,

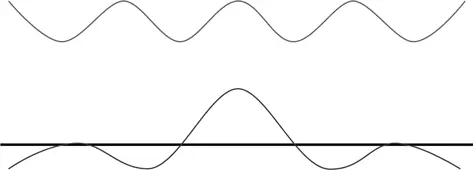
то результирующая волна будет выглядеть так:

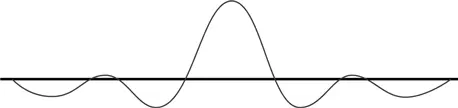
Интерференция размывает колебания еще сильнее, за исключением тех мест, где пики двух волн складываются, делая суммарную пиковую амплитуду волны намного выше, чем во всех остальных местах.

Можете сами представить, что произойдет, если я буду продолжать этот процесс, добавляя к первоначальной достаточно много других волн со слегка отличающимися частотами. Чем дальше, тем больше амплитуды волн будут гасить друг друга во всех точках, кроме некоторой небольшой области в центре рисунка и других отдаленных областей, где все пики могли бы вновь сойтись вместе.

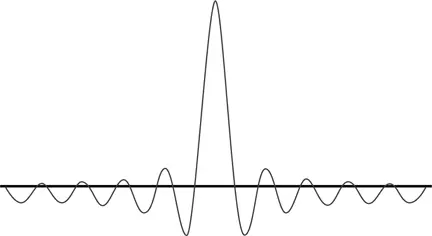
Чем больше число слегка различающихся частот, которые я складываю вместе, тем ýже окажется получившийся в итоге самый высокий центральный пик. А теперь представьте, что все это являет собой волновую функцию некой частицы. Чем больше амплитуда центрального пика, тем выше вероятность обнаружить частицу где-то в пределах ширины этого пика. Но ширина этого центрального пика все же никогда не становится совсем нулевой, так что возмущение остается распределенным по некоторой небольшой и все более сужающейся области.

Теперь вспомните: Планк и Эйнштейн рассказали нам, что, по крайней мере для световых волн, энергия каждого кванта излучения, то есть каждого фотона, прямо связана с его частотой. Неудивительно, что аналогичное соотношение действует и для волн вероятности, связанных с массивными частицами, но в этом случае с частотой, отвечающей частице волны, оказывается связан импульс частицы.

Отсюда и соотношение неопределенностей Гейзенберга: если мы хотим локализовать частицу в небольшой области, то есть получить как можно более узкий высочайший пик на ее волновой функции, то должны считать, что волновая функция получается сложением множества различных волн с чуть различающимися частотами. Но это означает, что импульс частицы, связанный с частотой ее волновой функции, должен быть несколько «размазан». Чем ýже доминантный пик волновой функции частицы, тем выше число различных частот (то есть импульсов), которые необходимо сложить, чтобы получить итоговую волновую функцию. Выражаясь более привычным языком, чем точнее мы хотим определить конкретное положение частицы, тем выше окажется неопределенность ее импульса.

Как видите, здесь нет никакого ограничения, связанного с реальными наблюдениями, или с сознанием, или с конкретными технологиями проведения наблюдений. Это свойство, неразрывно связанное с тем фактом, что в квантовом мире каждой частице соответствует волновая функция, а у частиц с фиксированным конкретным импульсом волновая функция характеризуется одной конкретной частотой.

Открыв это соотношение, Гейзенберг первым дал эвристичное объяснение его причин в форме мысленного эксперимента. Чтобы измерить положение частицы, вам нужно, чтобы от нее отразился свет, а чтобы узнать положение с высокой точностью, нужен свет с достаточно короткой длиной волны. Но чем меньше длина волны, тем больше частота и выше энергия, связанная с квантом данного излучения. Отражение света все более высоких энергий от частицы, очевидно, меняет ее энергию и импульс. Таким образом, после измерения вы сможете узнать положение частицы в данный момент, но при этом диапазон возможных энергий и импульсов, которые вы передали частице, рассеивая на ней свет, окажется довольно большим.

По этой причине многие путают соотношение неопределенностей Гейзенберга с так называемым «эффектом наблюдателя» в квантовой механике. Но, как видно из приведенного мной примера, по своей сути принцип неопределенности Гейзенберга не имеет никакого отношения к наблюдениям. Перефразируя слова одного моего друга, можно сказать, что если бы сознание играло роль в определении результатов квантово-физических экспериментов, то нам бы пришлось при публикации этих результатов обсуждать, о чем думал экспериментатор (к примеру, о сексе), проводя эксперимент. Но мы этого не делаем. Ведь очевидно, что взрывы сверхновых, породившие атомы, из которых состоит ваше и мое тело, вполне успешно произошли задолго до того, как возникло наше сознание.

Принцип неопределенности Гейзенберга во многих отношениях подводит черту под классической картиной мира. Вне зависимости от любых технологий, которые нам, возможно, когда-нибудь удастся создать, природа кладет абсолютный предел нашей способности одновременно и со сколько угодно высокой степенью точности знать импульс и положение любой частицы.

Но вопрос стоит даже более категорично, чем подразумевает это утверждение. Знание также не имеет к нему никакого отношения! Как я рассказал, описывая эксперимент с двумя щелями, не существует смысла, в котором частица в произвольный момент обладает одновременно точным положением в пространстве и точным значением импульса. Она обладает тем и другим в широком диапазоне в одно и то же время – до тех пор, пока мы не провели измерение и тем самым не зафиксировали по крайней мере один из этих параметров в узком диапазоне, определяемом качеством нашего измерительного оборудования.

Следующий после Гейзенберга шаг в раскрытии квантового безумия реальности сделал исследователь, от которого трудно было этого ожидать, – Поль Адриен Морис Дирак. Хотя в определенном смысле Дирак был идеальным кандидатом для этой работы. Говорят, Эйнштейн позже высказался о нем так: «Это постоянное балансирование на головокружительном пути между гениальностью и безумием ужасно».

Когда я думаю о Дираке, на ум приходит старый анекдот. Маленький ребенок не разговаривает, его родители бегают по врачам в поисках помощи, но ничто не помогает. И вот на свой четвертый день рождения он спускается к завтраку, поднимает глаза на родителей и говорит: «Тост остыл!» Родители прыгают от радости, обнимаются, а потом спрашивают ребенка, почему он никогда не говорил раньше. Он отвечает: «До сих пор все было в порядке».

Дирак славился своей лаконичностью, и существует немало историй о том, как он чурался всякого остроумия и вообще, кажется, воспринимал все сказанное ему буквально. Рассказывают, что однажды, когда Дирак во время лекции писал на доске, кто-то в аудитории поднял руку и сказал: «Я не понимаю вот этот шаг, который вы только что записали». Дирак очень долго стоял молча, пока тот человек в аудитории не спросил, собирается ли он отвечать на вопрос. На что Дирак ответил: «Никакого вопроса не было».