Лоуренс Краусс - Почему мы существуем? Величайшая из когда-либо рассказанных историй

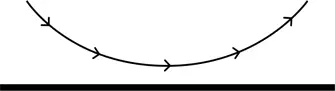
Французский математик Пьер де Ферма предложил в 1650 г. другой способ осмысления этого явления. Свет движется быстрее в теплом, менее плотном воздухе, нежели в холодном. Поскольку теплее всего воздух у поверхности, свету требуется меньше времени, чтобы попасть в ваш глаз по траектории, проходящей вдоль поверхности, чем напрямую. Ферма сформулировал принцип, получивший название принципа наименьшего времени , который гласит: чтобы определить итоговую траекторию любого светового луча, нужно просто проверить все возможные пути из точки A в точку B и найти тот из них, что требует наименьшего времени.

Формулировка звучит так, будто свет обладает собственной волей. Я с трудом удержался и не сказал, что свет рассматривает все возможные пути и выбирает тот из них, который требует наименьшего времени, поскольку уверен, что Дипак Чопра тут же процитировал бы меня и заявил, что я наделяю свет сознанием. Свет не имеет сознания, но математический результат выглядит так, будто свет выбирает самый быстрый путь.

А теперь вспомните, что в квантовой механике световые лучи и электроны движутся вовсе не по единственной траектории от точки к точке, а по всем возможным траекториям одновременно. Каждая траектория имеет определенную вероятность быть измеренной, но классическая, занимающая минимум времени траектория имеет самую большую вероятность из всех.

В 1939 г. Дирак предложил способ расчета всех таких вероятностей и их суммирования для определения квантово-механических шансов на то, что частица, вылетающая из точки A, в конечном итоге окажется в точке B. Ричард Фейнман, в то время студент-старшекурсник, услышав о статье Дирака на пивной вечеринке, математически вывел конкретный пример, на котором продемонстрировал, что эта идея работает. Взяв посыл Дирака в качестве стартового момента, Фейнман получил результаты, идентичные тому, что можно было получить с использованием подходов Шрёдингера и Гейзенберга, по крайней мере в простых случаях. Что еще важнее, Фейнман теперь мог использовать новую формулу «суммирования по траекториям» в применении к тем квантовым системам, которые невозможно легко описать или проанализировать другими методами.

В итоге Фейнман доработал свой математический метод, чтобы развить релятивистское уравнение Дирака для квантового поведения электронов до полностью непротиворечивой квантово-механической теории взаимодействия между электронами и светом. За эту работу, положившую начало теории квантовой электродинамики (КЭД), в 1965 г. он был удостоен Нобелевской премии, которую разделил с Джулианом Швингером и Синъитиро Томонагой.

Однако еще до завершения этой работы Фейнман описал интуитивную физическую причину, по которой теория относительности в сочетании с квантовой механикой непременно требует существования античастиц.

Рассмотрим электрон, движущийся вдоль некоторой возможной «квантовой» траектории. Что это означает? До тех пор пока я не пытаюсь измерить положение или скорость электрона в процессе его движения, он движется одновременно по всем возможным траекториям между двумя точками. Среди этих траекторий есть и неразрешенные в классической физике, поскольку при движении по ним нарушались бы такие принципы, как, например, запрет превышения скорости света, вытекающий из теории относительности. С другой стороны, принцип неопределенности Гейзенберга гласит, что, даже если я попытаюсь измерить характеристики электрона во время его движения на каком-то небольшом промежутке времени, его скорости все же останется присуща некоторая неопределенность, избавиться от которой невозможно. Так что даже если я буду измерять траекторию электрона в различных точках, я не смогу исключить возможность его странного неклассического поведения в промежутках. Представьте, к примеру, следующую траекторию.

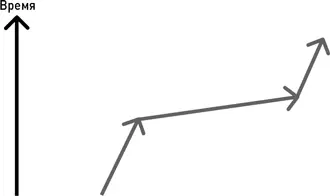
В течение короткого времени в середине изображенного периода электрон движется быстрее света.

Но Эйнштейн говорит нам, что время относительно, и разные наблюдатели измерят разные промежутки времени между событиями. А если какая-то частица движется быстрее света в одной системе отсчета, то в другой системе отсчета наблюдателю покажется, что она движется назад во времени, как изображено на следующем рисунке (это одна из причин, почему теория относительности ограничивает скоростью света движение всех наблюдаемых частиц).

Фейнман понял, что во второй системе отсчета это выглядело бы как электрон, который некоторое небольшое время движется вперед во времени, затем движется назад во времени, затем снова движется вперед. Но как выглядит электрон, который движется назад во времени? Поскольку электрон – отрицательно заряженная частица, отрицательный заряд, движущийся назад во времени слева направо, эквивалентен положительному заряду, движущемуся вперед во времени справа налево. Таким образом, наша схема эквивалентна следующей картине.

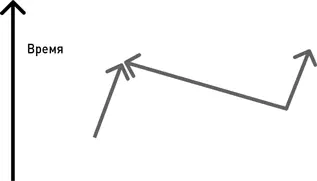
На этом рисунке все начинается с электрона, движущегося вперед во времени, но затем в какой-то момент из пустого пространства внезапно появляются электрон и еще одна частица, которая очень похожа на электрон, но обладает противоположным зарядом; после этого положительно заряженная частица движется влево, опять же вперед во времени, пока не встречается с первоначальным электроном и не аннигилирует с ним; в результате остается один электрон, который продолжает движение.

Все это происходит на таком масштабе времени, который невозможно наблюдать непосредственно, – ведь если бы все это можно было наблюдать, то такое странное поведение, нарушающее фундаментальные положения теории относительности, было бы невозможно. Однако можете быть уверены, что внутри бумаги в книге, которую вы сейчас читаете, или за экраном вашей электронной книги такого рода процессы происходят постоянно.

Но если такая траектория возможна в невидимом квантовом мире, то античастицы – частицы, идентичные известным частицам, но обладающие противоположным по знаку электрическим зарядом (в уравнениях этой теории они выглядят как частицы, движущиеся назад во времени), – должны существовать и в видимом мире. Это также делает возможным спонтанное возникновение в пустом пространстве пар частица-античастица, при условии что они аннигилируют за такое короткое время, чтобы их недолгое существование нельзя было измерить.