Ричард Фейнман - Том 3. Квантовая механика

Фиг. 2.8. Типы стоячих волн на отрезке.

Мы предпочитаем пользоваться волновым числом k =2π/λ; обозначая волновое число j -го типа колебаний через k j , получаем

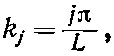(2.34)

где j — целое. Промежуток δ k между последовательными типами равен

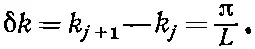
Нам удобно выбрать столь большое kL , что в малом интервале Δ k оказывается множество типов колебаний.

Обозначив число типов колебаний в интервале Δ k через Δℜ, имеем

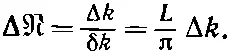(2.35)

Физики-теоретики, занимающиеся квантовой механикой, обычно предпочитают говорить, что типов колебаний вдвое меньше; они пишут

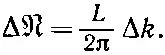(2.36)

И вот почему. Им обычно больше нравится мыслить на языке бегущих волн — идущих направо (с k положительными) и идущих налево (с k отрицательными). Но «тип колебаний», или «собственное колебание», — это стоячая волна, т. е. сумма двух волн, бегущих каждая в своем направлении. Иными словами, они считают, что каждая стоячая волна включает два различных фотонных «состояния». Поэтому если предпочесть под Δℜ подразумевать число фотонных состояний с данным k (где теперь уже k может быть и положительным, и отрицательным), то тогда Δℜ окажется вдвое меньше. (Все интегралы теперь нужно будет брать от k =-∞ до k =+∞, и общее число состояний вплоть до любого заданного абсолютного значения k получится таким, как надо.) Конечно, стоячие волны мы тогда не сможем хорошо описывать, но подсчет типов колебаний будет идти согласованно.

Теперь наши результаты мы обобщим на три измерения. Стоячая волна в прямоугольном ящике должна обладать целым числом полуволн вдоль каждой оси . Случай двух измерений дан на фиг. 2.9.

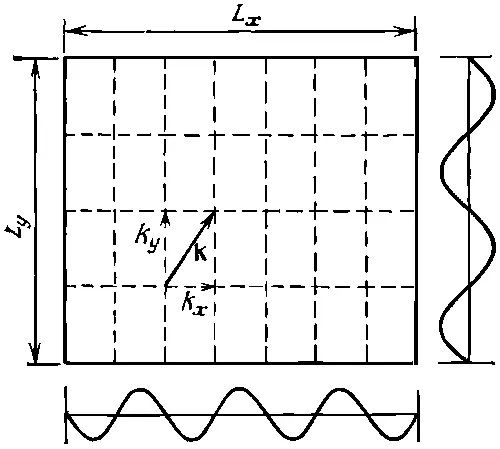
Фиг. 2.9. Типы стоячих волн в двух измерениях.

Каждое направление и частота волны описываются вектором волнового числа k. Его х -, у - и z-компоненты должны удовлетворять уравнениям типа (2.34). Стало быть, мы имеем

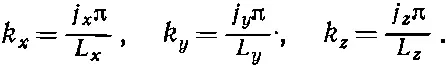
Число типов колебаний с k x в интервале Δ k x, как и прежде, равно

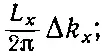
то же и с Δ k y, и с Δ k z. Если обозначить через Δℜ( k) число таких типов колебаний, в которых векторное волновое число kобладает х-компонентой в интервале от k x до k x+Δ k x, у-компонентой в интервале от k y до k y+Δ k yи z-компонентой в интервале от k z до k z+Δ k z, то

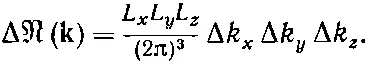(2.37)

Произведение L x L y L z — это объем V ящика. Итак, мы пришли к важному результату, что для высоких частот (длин волн, меньших, чем габариты полости) число мод (типов колебаний) в полости пропорционально ее объему V и «объему в k -пространстве» Δ k хΔ k yΔ k z. Этот результат то и дело появляется то в одной, то в другой задаче, и его стоит запомнить:

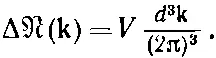(2.38)

Хоть мы этого и не доказали, результат не зависит от формы ящика.

Теперь мы применим этот результат для того, чтобы найти число фотонных мод для фотонов с частотами в интервале Δω. Нас интересует всего-навсего энергия разных собственных колебаний, а не направления самих волн. Мы хотим знать число собственных колебаний в данном интервале частот. В вакууме величина kсвязана с частотой формулой

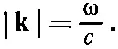(2.39)

Значит, в интервал частот Δω попадают все моды, отвечающие векторам k, величина которых меняется от k до k +Δ k независимо от направления. «Объем в k-пространстве» между k и k +Δ k — это сферический слой, объем которого равен

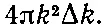
Количество собственных колебаний (мод) тогда равно

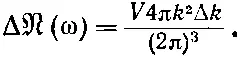(2.40)

Однако раз нас интересуют частоты, то надо подставить k =ω/ c , и мы получаем

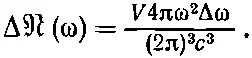(2.41)

Но здесь возникает одно усложнение. Если мы говорим о собственных колебаниях электромагнитной волны, то каждому данному волновому вектору kможет соответствовать любая из двух поляризаций (перпендикулярных друг другу). Поскольку эти собственные колебания независимы, то нужно (для света) удвоить их число. И мы имеем

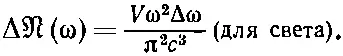(2.42)

Мы показали уже [см. (2.33)], что каждое собственное колебание (мода, тип колебаний, «состояние») обладает в среднем энергией

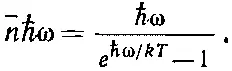
Умножая это на число собственных колебаний, мы получаем энергию Δ Е , которой обладают собственные колебания, лежащие в интервале Δω:

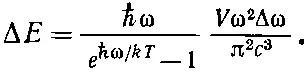(2.41)

Это и есть закон для спектра частот излучения абсолютно черного тела, найденный нами уже однажды в гл. 41 (вып. 4). Спектр этот вычерчен на фиг. 2.10.

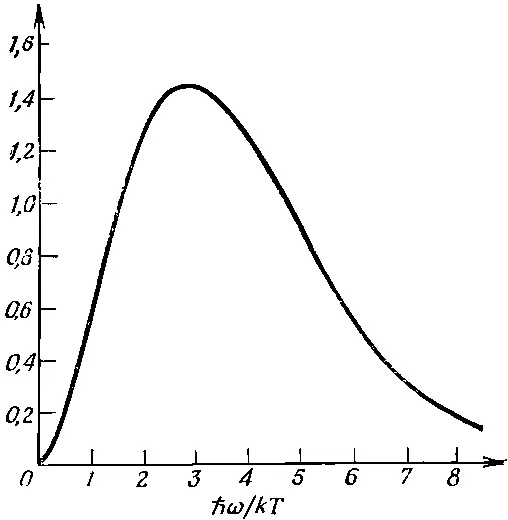
Фиг. 2.10. Спектр частот излучения в полости при тепловом равновесии (спектр «абсолютно черного тела»). На оси ординат отложена величина x 3 /e x —1 (x=ℏω/kT), отличающаяся от de/dω постоянным множителем (πℏ) 2 (c/kT) 3 V -1 .

Вы теперь видите, что ответ зависит от того факта, что фотоны являются бозе-частицами — частицами, имеющими тенденцию собираться всем вместе в одном и том же состоянии (амплитуда такого поведения велика). Вы помните, что именно Планк, изучавший спектр абсолютно черного тела (который представлял загадку для классической физики) и открывший формулу (2.43), положил тем самым начало квантовой механике.