Нил Тайсон - Большое космическое путешествие
- Название:Большое космическое путешествие
- Автор:
- Жанр:
- Издательство:Питер
- Год:2018
- Город:Санкт-Петербург
- ISBN:978-5-496-03227-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Нил Тайсон - Большое космическое путешествие краткое содержание
Астрономы не привыкли усложнять то, что может быть простым. Большие красные звезды – это красные гиганты. Маленькие белые звезды – это белые карлики. Если звезда пульсирует, она называется пульсар. Даже начало всего пространства, времени, материи и энергии, что существуют в космосе, можно назвать всего двумя простыми словами: Большой Взрыв.
Что мы знаем о Вселенной? Наша Вселенная велика. Наш Космос гораздо больше, чем кажется. Он жарче, чем вы думаете. Плотнее, чем вы думаете. Разреженнее, чем вы думаете. Что бы вы ни думали о Вселенной, реальность все равно окажется невероятнее.
Добро пожаловать во Вселенную!
Большое космическое путешествие - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
27
√1 – ( v 2/ c 2) = 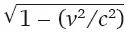
28
J.Richard Gott, “Will We Travel Back (or Forward) in Time?” Time Magazine , April 10, 2000, 68–70.
29
На самом деле предпоследней. – Примеч. пер .
30
Тензор кривизны Римана R αβγδв четырех измерениях содержит 256 компонент. Каждый из этих четырех индексов (один верхний и три нижних) – α, β, γ и δ – может принимать одно из четырех значений, соответствующих одному из четырех измерений пространства-времени ( t, x, y и z ). Получается 4 × 4 × 4 × 4 = 256 компонент. – Примеч. авт .
31
T μν – это тензор энергии-импульса, описывающий свойства материи в конкретной точке пространства-времени: плотность массы-энергии, давление, плотность, поток энергии и поток импульса. Параметр g μν, с которым мы уже сталкивались ранее (в плоском пространстве-времени он задается формулой ds 2= – dt 2+ dx 2+ dy 2+ dz 2), описывает, как измеряются расстояния в пространстве и промежутки времени. R μνи R можно вычислить по компонентам риманова тензора кривизны. У тензоров в уравнениях Эйнштейна по два индекса, каждый из которых может принимать любое из четырех значений. Таким образом, получается 4 × 4 = 16 уравнений. Десять из этих уравнений независимы. – Примеч. авт .
32
Из лекции, прочитанной в университете Глазго 20 июня 1933 года. Опубликовано в работе Эйнштейна The Origins of the Theory of Relativity , в оригинале цитируется по Mein Weltbild (Amsterdam: Querido Verlag, 1934), 138; и Ideas and Opinions (репринтное издание; New York: Broadway Books, 1995), 289–290.
33
Прозрачный намек на песню Hotel California. – Примеч. пер .
34
Из личной беседы с Доном Пейджем, учеником Хокинга. Он также рассказывает об этом в “Hawking Radiation and Black Hole Thermodynamics” Don N.Page, Alberta University, September 2004.Published in New Journal of Physics 7 (2005): 203, ALBERTA-THY-18-04 DOI: 10.1088/1367-2630/7/1/203, e-Print: hep-th/0409024 | PDF.Этот рассказ согласуется с данными из книги самого Хокинга «Краткая история времени», с.99–105.
35
Перевод Ильи Ратнера. В оригинале этот лимерик звучит так: There was a young lady of Wight // Who traveled much faster than light.// She departed one day, // In a relative way, // And arrived on the previous night. – Примеч. науч. ред.
36
Мы с Марком Олпертом исследовали, как во Флатландии будет действовать общая теория относительности. Мы обнаружили, что пространство вокруг точечной массы будет иметь коническую геометрию, а отдаленные объекты во Флатландии не будут притягиваться друг к другу, поскольку пространство там является локально плоским (то есть из листа бумаги можно изготовить конус, вырезав сегмент и склеив его края). Такое исследование Флатландии в конечном итоге вдохновило меня поработать над космическими струнами. Чтобы получить точное решение для космической струны, оказалось достаточно добавить вертикальную координату к решению, найденному для точечной массы во Флатландии. В данном случае такое исследование вымышленного мира натолкнуло нас на некоторые решения, представляющие интерес в реальном мире. Поскольку точечные массы во Флатландии не испытывают гравитационного притяжения друг к другу, в таком мире сложнее протекала бы агрегация массы, необходимая для образования планет. – Примеч. авт .
37
В 1984 году А.Дьюдни развил эту идею в своей книге «Планиверсум». В 2007 году на экраны вышел анимационный фильм по книге «Флатландия» с Мартином Шином и Кристен Белл в главных ролях, которые озвучили Артура Сквера (Квадрат) и его дочь Гекс (Шестиугольник). Когда я учился на старших курсах в Гарварде, один из моих наставников, Томас Бэнчофф, добавил на DVD специальные математические комментарии, которые были записаны на DVD отдельной дорожкой. – Примеч. авт .
38
По уточненным данным, полученным рентгеновской обсерваторией «Чандра» в 2011 г., масса Лебедь X-1 составляет 14,8 солнечной. – Примеч. пер .
39
В моей статье, опубликованной в 1982 году в журнале Nature , я написал: «Наша Вселенная – это один из обычных вакуумных пузырей». – Примеч. авт .
40
В той самой статье, написанной по мотивам исследований Сидни Коулмана о формировании пузырьков, я обозначил квантовое туннелирование как процесс, в результате которого должны возникать пузырьковые вселенные. «Следовательно, можно предположить, что наша Вселенная образовалась в результате квантового туннелирования». – Примеч. авт .
41
Статья Хокинга называлась «Формирование нерегулярностей в одиночной пузырьковой инфляционной вселенной», в ней были ссылки на работы Линде, Стейнхардта и Альбрехта, а также на мои. События того года описаны в книге Physics News in 1982 , опубликованной Американским институтом физики. На обложке этой книги использовалась ключевая схема из моей статьи. – Примеч. авт .
42
Эта тема подробно раскрыта в моей книге Cosmic Web (2016). – Примеч. авт .
43
Обозначения соответствуют английским названиям кварков: up, down, strange, charm, beauty, truth.Для двух последних есть альтернативные названия bottom и top, но в переводе на русский они путаются с верхним и нижним кварками, и потому этих названий избегают. – Примеч. науч. ред.
44
Все три сценария, w > –1, w = –1 и w < –1, а также их следствия, я еще подробнее рассмотрел в книге The Cosmic Web . – Примеч. авт .
45
Эти данные я опубликовал в журнале Nature 27 мая 1993 года в статье под названием Implications of the Copernican Principle for our Future Prospects. – Примеч. авт .
46
Насколько вероятно, что наш разумный род ( Homo Sapiens и его разумные потомки) просуществует вечно? Сейчас нашему роду около 200 тысяч лет. Это очень мало по сравнению с возрастом Вселенной, 1/65 000.По мере взросления нашего вида отношение его возраста к возрасту Вселенной должно стремиться к 1; если наши разумные потомки просуществуют вечно, то большинство наблюдателей обнаружит, что возраст их вида примерно такой же, как и возраст Вселенной. Вы такого не наблюдаете, и в этом вы особенны. Эту идею можно выразить количественно. Представьте себе двумерную систему координат, где по оси ординат отложен возраст Вселенной, при котором началась наша родословная в качестве разумного вида, а по оси абсцисс – наблюдаемый нами возраст Вселенной. Следовательно, каждая точка на плоскости – это возможная позиция наблюдателя. Но есть и ограничения. Оси x и y положительны (поэтому наш обзор ограничен верхней правой четвертью всей плоскости). Поскольку наблюдения должны происходить уже после того, как началась история разумного вида, истинно утверждение x > y .Поэтому зона наблюдений ограничена еще сильнее: речь идет о половине вышеупомянутой четверти или о 1/8 всей плоскости, а именно о восточном и северо-восточном октанте плоскости. Можно представить себе этот регион как 45-градусный лепесток, исходящий от начала координат до бесконечности, поскольку мы предполагаем, что наши разумные потомки просуществуют вечно. Наша точка наблюдения (с доступными нам значениями x и y ) может находиться где угодно в пределах этого 45-градусного лепестка. Если ваше наблюдение полностью заурядно, то должна существовать вероятность всего 1/45, что точка, в которой вы находитесь, окажется, например, в пределах 1° от ограничивающей диагональной линии x = y .Но на самом деле вы еще ближе к этой диагональной линии. Вы наблюдаете x = (1 + [1/65 000]) y .Эта точка ( x, y ), отложенная от начала координат, находится всего в 0,00044° от верхнего края (линии x = y ). При условии заурядности наблюдения вероятность оказаться настолько близко к краю составляет P = 0,00044°/45° = 10–5.Следовательно, если нашим разумным потомкам суждено существовать вечно, а наши наблюдения ничем не примечательны, то будет исключительно маловероятно (примерно 10–5), что возраст нашей разумной линии составит всего 1/65 000 от общего возраста Вселенной или менее. По принципу Коперника, исключительно маловероятно ( P = 10–5), что вы окажетесь в ситуации, когда ваше местоположение окажется особенным в соотношении 1/100 000 (здесь речь идет об эпизоде из родословной разумного вида, которому суждено просуществовать вечно). Следовательно, принцип Коперника, согласующийся со здравым смыслом, сообщает, что крайне маловероятно ( P = 10–5), что наши разумные потомки могут просуществовать вечно. В конце концов, формула Коперника (с 95-процентным доверительным интервалом) прогнозирует, когда наступит такой конец. – Примеч. авт .
Читать дальшеИнтервал:
Закладка:






![Нил Тайсон - Письма астрофизика [litres]](/books/1076565/nil-tajson-pisma-astrofizika-litres.webp)



