Лоуренс Краусс - Страх физики. Сферический конь в вакууме

Вода в критической точке и намагниченное железо в критической точке ведут себя похожим образом по двум причинам. Во-первых, флуктуации в критической точке происходят одновременно на всех масштабах, например, ни в каком объеме невозможно сказать о воде, в каком состоянии она находится: в жидком или в газообразном. Поскольку вещество выглядит одинаково на всех масштабах, локальные микрофизические свойства, такие как структура молекул, теряют свою актуальность. Во-вторых, все, чем характеризуется состояние воды в критической точке, это ее плотность, и даже не столько плотность, сколько отклонение плотности от средней величины в большую или в меньшую сторону. То есть вода в критической точке может быть полностью описана при помощи двух чисел: +1 и -1, и то же самое касается характеристики намагниченности железа в его критической точке.

Обе эти причины неразрывно связаны с симметрией. Вода и намагниченное железо в критической точке в некотором смысле подобны шахматной доске. Существуют только две степени свободы: черный и белый цвет клеток, повышенная или пониженная плотность, направление намагниченности вверх или вниз. Но ведь так бывает не всегда. Основной параметр, характеризующий возможные состояния системы вблизи критической точки, может иметь больше степеней свободы, например иметь величину и направление. Такая система будет выглядеть вблизи своей критической точки следующим образом:

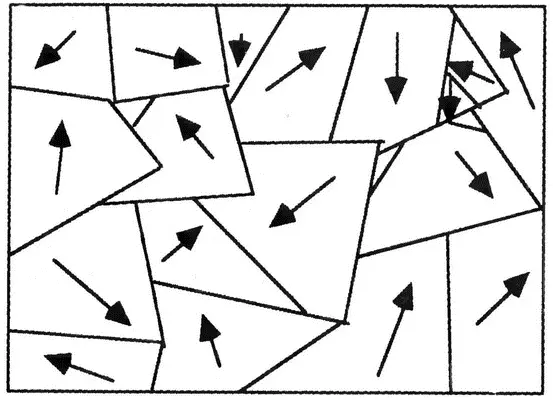
Вы можете подумать, что основные характеристики поведения такого материала вблизи критической точки будут отличаться от поведения воды или идеализированного куска намагниченного железа, и будете правы. Но в чем состоит главное различие между этим рисунком и рисунком, приведенным на странице 199? В наборе возможных значений параметра, описывающего фазовый переход. А что характеризует этот набор возможных значений? Основные симметрии этого параметра порядка. В зависимости от типа симметрии параметр порядка может принимать значения, соответствующие, например, координатам точки на окружности, на прямой, на сфере, в квадрате, в треугольнике и так далее.

Таким образом, мы опять видим, как симметрия определяет динамику процесса. Характер фазового перехода в критической точке полностью определяется характером параметра порядка. Но сам параметр порядка ограничен его симметрией. Вещества с одинаковой симметрией параметра порядка, претерпевая фазовый переход в критической точке, ведут себя одинаково. И в этом случае симметрия полностью определяет физику.

Такое использование симметрии позволяет нам увидеть подобие между физикой конденсированных сред и физикой элементарных частиц. На приведенном выше рисунке показано не что иное, как типичный пример спонтанного нарушения симметрии. Параметр порядка — вектор, характеризующий направление локальных магнитных полей, — может принимать любые направления. Он обладает внутренней круговой симметрией. После выстраивания элементарных «магнитиков» в одном направлении эта симметрия нарушается, спонтанно выбирая какое-то одно направление.

В приведенном выше примере в критической точке это направление постоянно меняется, и это происходит на всех масштабах, поэтому в критической точке все направления равноправны и симметрия не нарушена. Но вдали от критической точки система будет находиться в какой-то одной конфигурации, это может быть, например, жидкая вода или намагниченный в каком-то одном направлении кусок железа. В физике элементарных частиц мы поступаем похожим образом, описывая конфигурацию основного состояния Вселенной — вакуум — как некую когерентную конфигурацию элементарных полей, имеющих в этом состоянии некоторые фиксированные значения. Параметром порядка в этом случае являются величины самих элементарных полей. Если в низшем энергетическом состоянии они имеют ненулевое значение, то частицы, которые взаимодействуют с этими полями, будут вести себя иначе, чем частицы, которые с ними не взаимодействуют. Тогда существовавшие ранее симметрии, характеризующие эти элементарные частицы, нарушатся.

В итоге симметрия, проявляющаяся на малых масштабах, на которых флуктуации фоновых полей слишком сильны, чтобы согласованно влиять на поведение частиц, нарушается на больших масштабах, где локальные флуктуации усредняются. Кроме того, считается, что нарушенные ныне симметрии были ненарушенными на очень ранней стадии Большого взрыва, когда Вселенная была очень мала и крайне горяча. При расширении Вселенной в ней произошел фазовый переход, аналогичный переходу воды в жидкое состояние, когда температура опускается ниже критической точки. При достаточно высокой температуре могут проявляться нарушенные в обычном состоянии симметрии, потому что параметр порядка, характеризующий состояния элементарные полей, при высокой температуре обладает большим числом степеней свободы.

Сегодня принято считать, что для каждой известной нам симметрии существуют такие условия, в которых она нарушается, приводя к «фазовому переходу» в состоянии Вселенной. Большая часть сегодняшних исследований в области космологии посвящена изучению последствий таких фазовых переходов. И мы опять приходим к тому, что все в этом мире управляется симметрией.

Возвращаясь на Землю, мы обнаруживаем, что симметрия играет решающую роль в фазовых переходах, которые управляют поведением обычных веществ. Мы уже убедились, что симметрия параметра порядка воды, магнита или овсяной каши способна полностью определить поведение этих веществ в критических точках. Но, возможно, наиболее сильной из известных симметрии, определяющей саму нашу возможность описать эти переходы, является симметрия, с описания которой я начал эту книгу. Эта симметрия называется масштабной инвариантностью.

Главной особенностью любого вещества в критической точке является одинаковость его свойств на всех масштабах. Вещество становится масштабно-инвариантным: оно выглядит одинаково, независимо от того, под каким увеличением мы его рассматриваем. Это очень специфическое свойство, настолько специфическое, что им не обладают даже сферические кони!

Напомню, что я сумел сделать важные выводы биологического характера, рассматривая, как меняются свойства сферических коней при изменении их размера. Если бы соответствующая им физика оставалась масштабно-инвариантной, она разрешала бы существование сферических коней любой величины. Но это не так, потому что материал, из которого изготовлены кони, не изменяет свою плотность при увеличении размера коня. Из-за этого вес коня увеличивается пропорционально кубу его размера, в то время как сила его мышц растет пропорционально лишь квадрату размера.