Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Эратосфену было известно об этом из литературных данных. Отсюда следовало, что полуденное Солнце находилось в Сиене в этот день вертикально над головой наблюдателя. Эратосфен измерил в полдень того же дня длину тени, отбрасываемой обелиском в Александрии, и нашел, что направление солнечных лучей составляет 7 1/ 2° с вертикалью. Отсюда он заключил, что все солнечные лучи, падающие на Землю, параллельны. В этих опытах вертикали (радиус Земли) имели различные направления. Отсюда следовало, что радиусы Земли в Александрии и в Сиене пересекаются в центре Земли под углом 7 1/ 2°. Если этот угол в 7 1/ 2° соответствует 500 милям на поверхности Земли, то скольким милям будут соответствовать 360°? Остальное уже сводилось к простой арифметике. Измерить расстояние в 500 миль в те времена было трудно — вероятно, — такие измерения производились военными, чеканившими шаг. Имеются сомнения по поводу единиц, которыми пользовался Эратосфен, но по некоторым сведениям его ошибка была меньше 5 % — замечательный успех столь ранней попытки. Эратосфен пытался также определить расстояния до Солнца и Луны.

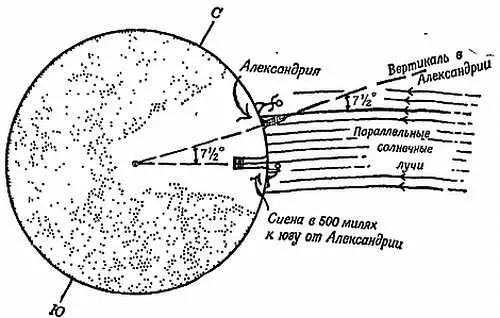
Фиг. 37. Определение размеров Земли по Эратосфену.

Размеры Луны и ее расстояние от Земли

Размеры Луны сравнивались с размерами Земли путем наблюдения лунных затмений. Отмечая время, в течение которого тень Земли пересекала Луну, Аристарх нашел, что диаметр тени, отбрасываемой Землей на Луну, в 2 1/ 2раза больше диаметра Луны. Если бы Солнце представляло собой точечный источник света, находящийся на бесконечно большом расстоянии, то Земля отбрасывала бы от падающего на нее потока параллельных солнечных лучей тень, поперечное сечение которой равнялось бы поперечнику Земли. В этом случае мы имели бы:

ДИАМЕТР ЗЕМЛИ = 2 1/ 2ЛУННЫХ ДИАМЕТРА,

или

ДИАМЕТР ЛУНЫ = 2/ 5ДИАМЕТРА ЗЕМЛИ,

т. е.

РАССТОЯНИЕ ОТ ЗЕМЛИ ДО ЛУНЫ, РАВНОЕ 110 ЛУННЫМ ДИАМЕТРАМ

= ( 2/ 5)∙110 ЗЕМНЫХ ДИАМЕТРОВ

= 44 ЗЕМНЫМ ДИАМЕТРАМ, ИЛИ 88 ЗЕМНЫМ РАДИУСАМ.

Отсюда следует, что если принять радиус Земли равным, согласно Эратосфену, приблизительно 4000 миль, то расстояние от Земли до Луны должно быть равно 350 000 миль. Предположение, что Солнце находится на бесконечности, представляется разумным, однако было бы неправильно считать его точечным источником, и Аристарх, конечно, это знал. Солнце — огромный пылающий шар, и поэтому тень от Земли (или другой планеты), на которую падает поток солнечных лучей, будет иметь коническую форму (с углом раствора ~ 1/ 2°). При полном солнечном затмении Луна может лишь закрыть Солнце от наших глаз, причем конус лунной тени будет кончаться практически у Земли. На расстоянии от Луны до Земли тень от Луны суживается на целый лунный диаметр.

При лунном затмении ширина земной тени, отбрасываемой на то же расстояние (от Земли до Луны), должна уменьшиться на ту же величину, т. е. на лунный диаметр. Аристарх рассуждал следующим образом:

ДИАМЕТР ЗЕМЛИ — ОДИН ДИАМЕТР ЛУНЫ = 2 1/ 2ДИАМЕТРАМ ЛУНЫ,

т. е.

ДИАМЕТР ЗЕМЛИ = (1 + 2 1/ 2) ДИАМЕТРАМ ЛУНЫ

= 7/ 8ДИАМЕТРА ЛУНЫ

или

РАССТОЯНИЕ ОТ ЗЕМЛИ ДО ЛУНЫ = 110 ДИАМЕТРАМ ЛУНЫ

= ( 2/ 7)∙(110) ДИАМЕТРАМ ЗЕМЛИ

= 31,4 ДИАМЕТРА ЗЕМЛИ, или 63 РАДИУСАМ ЗЕМЛИ.

Более точные измерения, выполненные Аристархом и его последователями, показали, что расстояние от Земли до Луны равно 60 земным радиусам (что с точностью до 1 % совпадает с современными измерениями), т. е. около 240 000 миль.

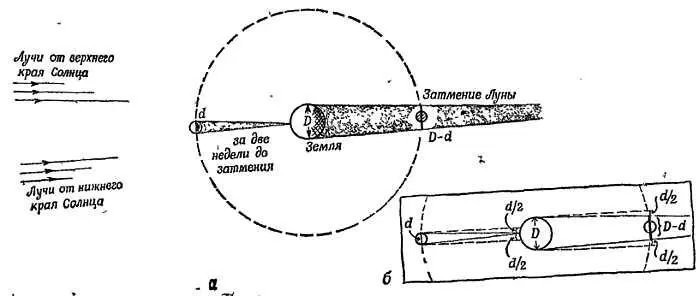
Фиг. 38. Измерение размеров Луны (и, следовательно, расстояния до нее) древними греками.

Наблюдения затмений показали, что ширина тени, отбрасываемой Землей на Луну, равна 2,5 диаметра Луны. Однако тень Земли сужается по мере того, как увеличивается расстояние до Земли, потому что Солнце — не точечный источник. Тень Луны почти исчезает на расстоянии от Луны до Земли, поэтому тень от Земли должна сузиться на ту же величину (один лунный диаметр) на этом расстоянии. Следовательно, диаметр Земли должен равняться 3,5 лунного диаметра.

Позднее расстояние от Земли до Луны было измерено следующим образом: наблюдатели на двух удаленных друг от друга пунктах, на одной долготе одновременно наблюдали Луну. Они измеряли угол между направлением, под которым была видна Луна , и между вертикалью в данной местности. Зная эти углы u и v , можно было определить положение Луны, если известно расстояние между пунктами. Большое расстояние измерить древним астрономам было трудно, но можно было воспользоваться вместо этого углом между радиусами Земли, соответствующими двум пунктам. Так что наблюдатель в каждом пункте измерял угол между местной вертикалью и тем направлением, под которым он видит определенную звезду.

Для этой цели подходит Полярная звезда или любая другая, наблюдаемая в своей наивысшей точке. Как показано на фиг. 39, б , сумма двух измеренных углов ( х + у ) дает угол z в центре Земли. На фиг. 39, в изображены три известных угла u, v, z ; известно также, что радиусы R равны. Чтобы найти расстояние от Земли до Луны, можно либо прибегнуть к тригонометрии, либо сделать в масштабе простой чертеж (фиг. 40) на большом листе бумаги (древние астрономы пользовались насыпанным на пол песком) — нарисовать круг и провести радиусы ОА и ОБ , образующие угол z , равный сумме измеренных углов х + у . Нужно продолжить эти радиусы, чтобы они представляли вертикали в пунктах А и В . Из А следует провести линию до Луны АР , измерив угол u , который она образует с радиусом ОА , а из B провести прямую BQ . Точка пересечения этих прямых М определяет положение Луны на диаграмме. Измерив отрезок ОМ и разделяв его на радиус ОА , получим расстояние от Луны до Земли как кратное радиусу Земли.

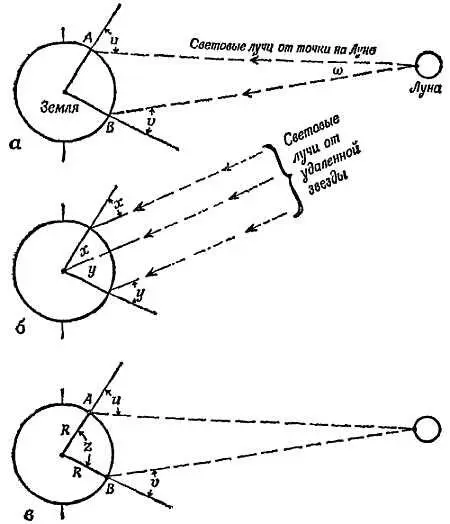
Фиг. 39. Измерение расстояния от Земли до Луны.

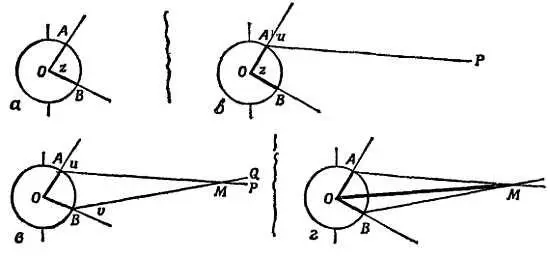
Фиг. 40. Вычисление отношения расстояния до Луны к радиусу Земли на основании измерений.

Точные измерения дают:

РАССТОЯНИЕ ОТ ЗЕМЛИ ДО ЛУНЫ = ОКОЛО 60 РАДИУСОВ ЗЕМЛИ

~= 240 000 миль.

Размеры Солнца и его расстояние от Земли

Расстояние от Земли до Солнца оценить гораздо труднее даже сегодня, ибо Солнце крайне ярко, велико и очень удалено от нас.