Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Угол между лучами зрения глаз при наблюдении Солнца слишком мал, чтобы его можно было измерить, не прибегая к телескопу. Однако Аристарх придумал остроумную схему, с помощью которой удалось, хотя и очень приближенно, оценить расстояние от Земли до Солнца. Он наблюдал за Луной в той стадии, когда видна точно ее половина (фиг. 41).

Фиг. 41. Расстояние от Земли до Солнца.

Определение расстояния от Земли до Солнца по известному расстоянию от Земли до Луны греческими астрономами. Они пытались измерить угол х (или SEM ), который равен приблизительно 90°.

Солнечный свет должен падать на Луну под прямым углом к ЕМ (направлению взгляда наблюдателя). В этот момент наблюдатель измеряет угол между направлениями от Земли к Солнцу и от Земли к Луне. Этот угол, SEM , оказался почти (но не совсем точно) прямым. В большом треугольнике SEM два угла были известны. Третий малый угол, ESM , в основном и определяет расстояние от Земли до Солнца. Он получается вычитанием из 180° и очень мал: по оценке Аристарха он равен 3°, на самом же деле всего 1/ 6°. Поэтому вывод Аристарха о том, что расстояние от Земли до Солнца примерно в 20 раз больше, чем до Луны, был занижен приблизительно в 20 раз. Это соотношение ( расстояние до Солнца )/( расстояние до Луны ) получается от рассмотрения углов на чертеже соответствующего масштаба или с помощью очень простой тригонометрии ( EM / ES — косинус угла SEM . Поэтому ES/ EM= 1/cos L SEMлегко находится из тригонометрических таблиц).

Таким образом, астрономам в Александрии были известны приближенные значения размеров небесной системы и этими значениями (с незначительными изменениями) пользовались астрономы в течение многих столетий:

Земля: радиус 4000 миль.

Луна: расстояние от Земли 60 земных радиусов, или 240 000 миль; собственный радиус 1100 миль.

Солнце: расстояние от Земли 1200 земных радиусов (это значение считалось неточным, каким оно и было); собственный радиус 44 000 миль.

Планеты: расстояния до них были совершенно неизвестны, но предполагалось, что все они находятся дальше, чем Луна.

Звезды: расстояния до них также были совершенно неизвестны, предполагалось, что они находятся за Солнцем и планетами.

Из этих оценок видно, что на рисунках, иллюстрирующих затмения, обычно совершенно не выдержан масштаб. Фиг. 42 и 43 дают более близкие к действительности схемы, основанные на современных измерениях. Не удивительно, что затмения происходят столь редко. Призрачных конусов теней можно и не заметить. Орбита Луны наклонена под углом 5° к видимой траектории Солнца, поэтому затмения происходят еще реже.

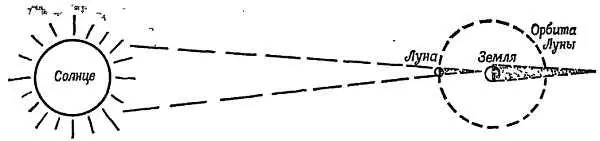
Фиг. 42. Солнце, Луна, Земля.

Чертеж дан не в масштабе. Солнце расположено слишком близко к Земле. Луна чрезмерно велика и расположена слишком близко к Земле.

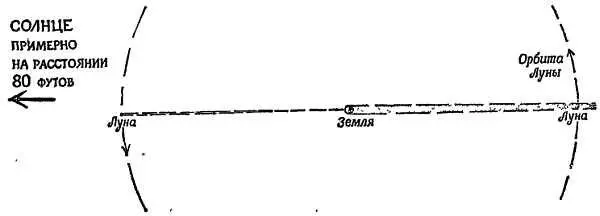
Фиг. 43. Конусы теней Луны и Земли (в масштабе).

Более поздние теории

Смелое предположение о том, что Земля вращается и движется вокруг Солнца, не было встречено благосклонно Александрийской школой. По-прежнему оставалось популярным представление о том, что Земля покоится и находится в центре мироздания, однако модель с вращающимися концентрическими сферами была слишком сложной. Не совсем равномерное движение Солнца по «орбите» можно было описать, используя эксцентрическую окружность: согласно этой модели, Солнце движется по такой окружности равномерно. Земля же неподвижна и находится не в центре круга, а на некотором расстоянии от него. При этом, если наблюдать за Солнцем с Земли, будет казаться, что оно движется быстрее в некоторые времена года (примерно в декабре, в точке А ) и медленнее на 6 месяцев позднее (в точке В ). Это была неплохая теория. Теория должна быть простой и основываться на простых допущениях [23] Допущения, говоря на научном языке, должны быть логичными. Такая формулировка озадачила бы древних мыслителей. Они считали, что логическим должен быть вывод из допущений. .

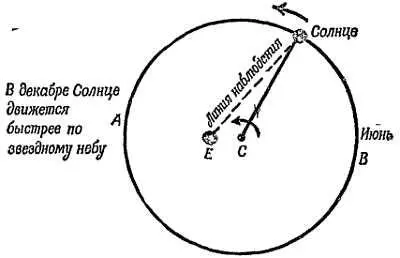
Фиг. 44. Схема эксцентрической орбиты Солнца.

Солнце движется по окружности, находясь на конце радиуса; который вращается с постоянной скоростью, как в простейшей системе сфер. Наблюдатель на Земле находится не в центре, поэтому движение Солнца ему кажется неравномерным, как в действительности и происходит — быстрее в декабре, медленнее в июне.

Эти требования удовлетворялись: движение по окружности с постоянным радиусом происходило с постоянной скоростью. Это постоянство было необходимо с точки зрения древних греков, а фактически с точки зрения каждого методически мыслящего ученого. Без него теория превратилась бы в нечто бесформенное.

Поместить Землю не в центре круга означало досадное отклонение от симметрии, но и скорость Солнца при этом оказалась несимметричной — наше лето продолжительнее зимы. Аналогичная схема была пригодна и для Луны, для планет же требовалась более сложная схема. Каждая планета должна была равномерно двигаться по кругу, совершая полный оборот в течение собственного «года» вокруг неподвижной Земли, находящейся не в центре этого круга, а на некотором расстоянии от него, но тогда весь круг, орбита планеты и центр круга должны совершать полный оборот вокруг Земли за 365 дней. Таким образом, к основному вращению добавлялось еще одно (по окружности радиуса ЕС ), в результате чего планета двигалась по эпициклоиде. На это движение накладывалось суточное движение всей звездной картины.

В другой схеме, приводившей к аналогичным результатам, вводился неподвижный главный круг (деферент) с радиальным плечом, вращающимся с постоянной скоростью. Конец плеча несет на себе малый круг (эпициклоиду). Радиус этого малого круга несет на себе планету, которая движется с постоянной скоростью, совершая один оборот за 365 дней. Хотя эти схемы оперируют с кругами, в них по-прежнему употребляли термин «сферы». В течение многих столетий астрономы привыкли рассматривать «движение небесных сфер», а сферы сами становились все более и более реальными по мере того, как восхищение греков чистой теорией уступало место детской настойчивости в поисках истины.