Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Различие этих выводов свидетельствует, что относительная скорость наблюдателей ε и ε ' равна v 0. Однако никакой информации об абсолютном движении здесь не содержится. Наблюдатель ε ' может стоять на месте, в этом случае наблюдатель ε бежит назад с постоянной скоростью v 0(запуская в момент t = 0 на бегу ракету, фиг. 131, б ). А может быть, оба наблюдателя, и ε и ε ', находятся в поезде, мчащемся с огромной скоростью (фиг. 131, в ), но и тогда ε движется со скоростью v 0относительно ε '. В любом случае v 0 будет относительной скоростью наблюдателей и никакой анализ их измерений не может сказать нам (или им), кто из них «действительно» движется.

Добавка v 0 t только сдвигает график зависимости s от t , но не влияет на ускорение и силы . Следовательно, на вопрос: «С какой скоростью движемся мы в пространстве?», простая механика отвечает: «Никакие эксперименты с весами, пружинами и силами… не могут выявить нашей скорости . Ускорение дает о себе знать, но постоянную скорость мы не чувствуем». Мы можем измерять только относительную скорость , т. е. скорость по отношению к другим телам и системам отсчета.

Тем не менее мы все же рассуждаем так, как будто бы существует абсолютное движение, как будто бы мимо нас проносятся «верстовые столбы» пространства, но как их заметить? Однако прежде чем перейти к этому вопросу, где нас ждет большее разочарование, мы запишем правила относительного движения в простой алгебраической форме.

Фиг. 133. Обнаружение одинаковых механических законов.

Галилеево преобразование координат

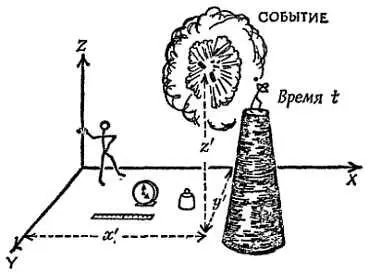
Сравнение результатов двух наблюдателей можно провести просто и в общем виде. Допустим, наблюдатель в описывает события в своей лаборатории. Другой наблюдатель ε ', пролетающий мимо лаборатории с постоянной скоростью v , описывает те же события так, как видит их он. Оба наблюдателя ε и ε ' приготовили для измерения одинаковые часы и метры и с каждым из них связаны оси X, Y и Z . Для удобства наблюдатели запускают свои часы ( t = 0, t ' = 0) в тот момент, когда находятся рядом. В тот же момент совпадают начала их систем и оси координат. Допустим, что, по мнению ε , событие произошло в момент t в точке ( х, у, z ) по отношению к своим осям [247]. Наблюдатель ε ' регистрирует то же событие с помощью своих приборов: оно происходит в момент t и в точке ( х ', у ', z ') по отношению к движущимся вместе с ним осям координат. Как сравнить эти два результата? Здравый смысл говорит нам, что время для обоих наблюдателей будет одним и тем же, так что t = t '. Пусть относительная скорость наблюдателей равна v = м/сек и направлена вдоль оси Х . Тогда координаты у и z для них будут также одинаковы: у ' = у , a z ' = z . Но поскольку наблюдатель ε ' вместе со своей системой координат переместился за время t от наблюдателя в на vt метров, его координаты х ' будут на vt метров меньше, так что каждое х ' должно быть равно х — vt . Итак,

х' = х— vt, y' = y, z' = z, t' = t.

Эти соотношения, связывающие результаты наблюдений ε и ε ', называются преобразованиями Галилея.

Обратные преобразования, связывающие наблюдения ε и ε ', имеют вид

х= х' + vt, y= y', z= z', t = t'.

Оба типа преобразований равноправны для обоих наблюдателей и указывают просто на наличие относительной скорости наблюдателей + v в случае ε ' —> ε и — v в случае ε —> ε '. Эта алгебраическая запись отражает наш обыденный взгляд на пространство и время.

Фиг. 134.

Скорость движущегося тела

Если наблюдатель ε видит движущееся вдоль оси X тело и измеряет его скорость и отношением Δ х /Δ t , то, по мнению ε ', то же тело движется со скоростью u ', равной Δ х '/Δ t '. Использование алгебры и преобразований Галилея показывает, что u' = u— v. (Чтобы получить это соотношение в случае постоянных скоростей, надо просто разделить х' = х— vtна t .)

Предположим, например, что наблюдатель ε стоит у железнодорожного полотна и видит движущийся со скоростью v = 100 км/час. Другой наблюдатель ε ' едет на товарном поезде со скоростью 40 км/час в том же направлении (фиг. 138).

Тогда экспресс с точки зрения ε ' будет двигаться со скоростью

u' = u— v= 100 — 40 = 60 км/час.

Если наблюдатель ε ' движется в противоположную сторону, как при лобовом соударении, то v = —40 км/час, и ε ' видит экспресс приближающимся со скоростью

u' = 100 — (—40) = 140 км/час.

Это обычный способ сложения и вычитания скоростей. Он кажется о точки зрения «здравого смысла» единственно правильным, и в первых главах (т. 1) мы принимали его как нечто непреложное. Тем не менее окажется, что при очень больших скоростях его необходимо модифицировать.

Абсолютное движение?

Если мы обнаружим, что лаборатория находится в движущемся поезде, то сможем учесть скорость движения поезда и отнести результаты всех наших опытов к Земле. Обнаружив движение Земли, мы можем поместить систему координат на Солнце, затем на звезды, затем в центр тяжести всех звезд. Но если эти перемены не влияют на наше понимание механики, имеют ли они смысл? Разумно ли так беспокоиться об абсолютной неподвижной системе?

Ответить заставляет любопытство. «Да. Если мы движемся в космическом пространстве, то было бы интересно знать, с какой скоростью». Если этого не могут сказать механические опыты, то, может быть, могут прояснить опыты с электричеством? Для неподвижного наблюдателя электромагнитные явления целиком содержатся в уравнениях Максвелла. Посмотрим, что обнаружит движущийся наблюдатель при переходе от х к х ' в соответствии с преобразованиями Галилея. Уравнения Максвелла тогда принимают более сложную форму. Доверяющий этим преобразованиям: экспериментатор сможет определить, что на самом деле движется — он или его приборы. Абсолютное движение проявилось бы в изменении формы законов теории электричества. Простейший способ найти эти изменения — воспользоваться распространением световых волн — электромагнитных полей, предсказанных уравнениями Максвелла.