Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Масса элемента = 3∙10 7/9,8 ~= 3∙10 6~= 3000 т. Так что это 3000-тонный (размером с дом) кусок скалы или соответственный объем воды или даже воздуха.

У берегов, где есть заливы и узкие горловины, приливы могут подниматься на большую высоту, а у островов, в открытом океане сизигийные приливы поднимаются только на 1,3 м; высота подъема квадратурного прилива вдвое меньше. Поэтому прилив, обусловленный Солнцем и Луной, достигает 1,3 м, а прилив, происходящий тогда, когда Солнце и Луна действуют в разные стороны, поднимается лишь на 0,6 м. Отсюда следует, что высота солнечного прилива 0,35 м, а высота лунного 0,95 м. Таким путем мы можем оценить отношение масс Луны и Солнца. Однако задача оказывается очень сложной.

Если мы зададим такой же вопрос, какой задавали Ньютону его коллеги: «Если принять закон обратных квадратов для притяжения, то по каким траекториям будут двигаться планеты и кометы?», то получим ответ: «Орбита будет коническим сечением, в одном из фокусов которого находится Солнце». Конические сечения — кривые, получающиеся при пересечении кругового конуса плоскостями.

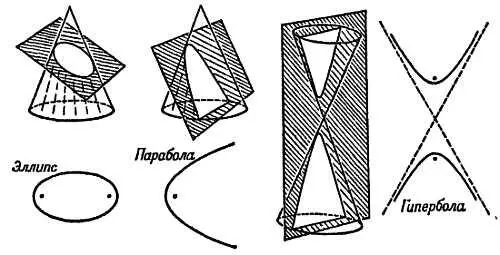
Фиг. 175. Конические сечения.

Конус, пересеченный плоскостью, перпендикулярной его оси, даст окружность . Если плоскость, пересекающая конус, по отношению к его оси наклонена, то получается эллипс . Если наклон плоскости еще больше и она параллельна образующей конуса, то получается парабола . Сечение с еще большим наклоном плоскости дает гиперболу . Эти кривые принадлежат к одному математическому семейству. Их алгебраические уравнения сходны:

Окружность: x 2+ y 2 = 9

Эллипс: x 2/9 + y 2/4 = 1

Гипербола: x 2/9 — y 2/4 = 1

Уравнение параболы выглядит по-другому (т. е. x 2 = 9 y), но также связано с остальными. В физике мы встречаемся с эллипсом, изучая орбиты планет; все эти кривые встречаются среди орбит комет, а гиперболы — в том случае, когда атомное ядро бомбардируется α-частицами (α-частицы движутся по гиперболам). Измеряя рассеяние α-частиц на атомных ядрах, можно рассчитать рассеивающие силы. Эти силы подчиняются закону обратных квадратов, действующему между α-частицей и ядром атома. Мы приходим к выводу, что эти силы есть результат электростатического отталкивания между электрическими зарядами. Из дальнейших намерений мы можем даже оценить электрические заряды атомных ядер. Это пример того, как механика Ньютона в наши дни помогает изучать атом.

Гл. 33 (« Электростатика. Электрические заряды и поля ») входит в т. 3 настоящего издания.

Расстояние между ними изменяется от величины, равной сумме радиусов орбит, до величины, равной их разности: 1400 млн. км — 770 млн. км (1400—770); отношение этих величин 3,5:1.Это вызывает возмущающее притяжение, меняющееся в отношении 1:12.

J. М. Кеуnes , Newton the Man, в кн. Newton Tercentenary Celebrations of The Royal Society of London, Cambridge, 1947.

Этот расчет был решающей проверкой великой теоретической идеи. Вы должны выполнить все арифметические действия очень точно, иначе это будет простой потерей времени. Ответы на два поставленных в задаче вопроса должны быть получены с тремя значащими цифрами (это потребует пяти десятичных порядков в значениях величин с размерностью м/сек 2). Вначале получите ответы в буквенных выражениях, без каких-либо сокращений, а затем — численный результат.

В задачах требуется очень приблизительный результат, дающий лишь общее понятие об относительных массах или величинах некоторых сил; точных арифметических вычислений не требуется, поэтому советуем учесть следующее:

A. Пользуйтесь алгебраическими выкладками до тех пор, пока это возможно .

Б. После этого подставьте арифметические величины, не сокращая их, и представьте результат со всеми коэффициентами . (Не сокращайте этот первый результат, а оставьте его нетронутым на тот случай, если вам понадобится к нему вернуться или потребуется его проверить.)

B. Перепишите «результат» пункта Б и сделайте грубую аппроксимацию, чтобы получить весьма приближенный ответ. Ниже даны три схемы аппроксимации:

а) Используйте грубые арифметические подсчеты. Это даст удовлетворительные результаты быстрее, нежели что-либо другое, если не считать специальных приемов и опыта. (Сведите все данные к степеням 2 или 10, а затем сокращайте. Помните: 2 10~= 10 3.)

б) Пользуйтесь таблицами логарифмов. Достаточны логарифмы с двумя десятичными знаками,

в) Используйте логарифмическую линейку. Делайте грубые прикидки для определения первого десятичного знака.

Если ваш результат больше или меньше верного в 1000 раз, то он бесполезен, если же только на 40 % за счет неточности в выкладках, то он дает полезные данные.

Гл. 10 (« Колебания и волны ») входит в т. 1 настоящего издания.

Гл. 10 (« Колебания и волны ») входит в т. 1 настоящего издания.

Гл. 39 (« Радиоактивность ») входит в т. 3 настоящего издания.

Вообразим себе такую схему. Предположим, что величина G медленно уменьшается в соответствии с показаниями «атомных» часов. Маятниковые часы, показывающие гравитационное время в прошедшие времена, должны были идти быстрее (такое заключение делается на основе вращения Земли или по атомным часам). Тогда Земля в прошедшие времена должна была бы вращаться медленнее (судя по маятниковым часам). Примем гравитационное время, показываемое маятниковыми часами, за относительный стандарт и будем наблюдать за изменениями времени в атомной шкале. (Ни одну из этих шкал времени нельзя считать истинной по сравнению с другой — только предубеждение заставляет нас считать, что атомное время более правильно и течет с постоянной скоростью.)

Представим себе, например, что соотношение между этими двумя шкалами времени «экспоненциальное», так что атомные часы по сравнению с маятниковыми удваивают свою скорость за триллион «маятниковых дней». Мы выбираем это одно из бесчисленного количества возможных соотношений просто для иллюстрации. Чтобы эта иллюстрация была еще проще, вообразим, что скользящая шкала, связывающая эти две системы часов, изменяется не плавно, а скачками, так что после каждого триллиона дней по маятниковым часам атомные часы внезапно удваивают свою скорость — вдвое чаще тикают за маятниковый день, чем прежде. (Такая схема скачков безнадежно маловероятна. Математические расчеты легче проводить как раз для случая гладкой экспоненциальной зависимости, которая может быть ближе к истине.) Тогда мы найдем, что для каждого триллиона дней, которые мы отсчитываем в прошлое по маятниковым часам, атомные часы работали бы вдвое медленнее, т е. за каждый маятниковый день было бы вдвое меньше тиканий атомных часов.