Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Как на юмористической картинке, изображающей лыжню на горном склоне, две линии которой разделяются и проходят с двух сторон сосны, а затем соединяются снова.

Чтобы увидеть кольцевую стоячую волну, налейте до половины воду в круглую стеклянную бутылку. Резко сообщите бутылке небольшое вращательное движение и найдите частоту, при которой у стенок бутылки на поверхности воды образуется стоячая волна. Более детальную иллюстрацию стоячих волн см. в гл. 10 .

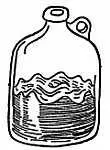
Фиг. 205.

Здесь «сила» измеряется КВАДРАТОМ (модуля) АМПЛИТУДЫ этой волны. (По существу, речь идет об интенсивности волны. — Прим. ред .)

Вряд ли можно признать убедительным или хотя бы правильным такое объяснение принципа Паули. Дело обстоит гораздо сложнее (например, фотоны и π -мезоны хотя и обладают волновыми свойствами, но не подчиняются принципу Паули), поэтому на первом этапе принцип Паули удобнее рассматривать как исходный закон, не требующий теоретических обоснований. — Прим. перев .

Чтобы проследить за соответствующим рассмотрением, нам нужны такие математические средства, излагать которые здесь у нас нет возможности. Этим объясняются смутность и неясность нашего описания, которое не определяет точно новую теорию.

Докажем это соотношение для фотона следующим образом: пусть квант света имеет энергию E= hv = mc 2и импульс mс или Е / с , где m — его масса.

Следовательно, неопределенность импульса составляет

Δ( m∙ c) = Δ( E/ c)

Скорость фотона равна с ; следовательно, если проделанный им путь известен с точностью Δ( x ), то время известно с точностью Δ( t) = Δ( x)/ c.

Следовательно, неопределенность Δ( x) = c∙Δ( t). Отсюда

Δ( m∙ c)∙Δ( x) = Δ( E/ c)∙ c∙Δ( t).

Если Δ( m∙ v)∙Δ( x) ~ h, то тогда Δ( Е)∙(Δ( t) ~ h

Если энергия фотона (и, следовательно, его частота и длина волны) измеряется достаточно точно, скажем с точностью 1 %, то Δ( E) = E/100 и Δ( t ) должна быть больше h /( E /100), или 100∙ h / E ∙(100∙ h / hv ), или 100/ v , т. е. 100 полных периодов колебаний волны. Для измерения Е (или v ) с точностью 1 % необходимо затратить такое время.

Анализ того лучшего, на что можно надеяться, иногда приводит к соотношению Δ( x)∙Δ( m∙ v) ~= h/2π, т. е. в лучшем случае к выигрышу на множитель, равный 6.

Для приборов в человеческий рост неопределенность Δ х может оказаться лишь ничтожной долей высоты объекта, а неопределенность Δ( mv ) — ничтожной частью его импульса (напомним, что масса объекта огромна), и тем не менее их произведение будет во много раз больше h . Например, попробуйте произвести измерения над бейсбольным мячом, масса которого 0,2 кг, движущегося со скоростью 3 м/сек. Предположим, что его положение удалось определить с точностью до длины волны зеленого света (лучшее, что можно получить с помощью оптического микроскопа). Тогда неопределенность Δ х равна 5000 А°, или 5∙10 -7м. Далее, предположим, что время его полета на расстояние 1 м нами определяется с точностью до 1/1 000 000 сек (максимум, на что можно надеяться для такого большого объекта). Тогда точность, с какой известна его скорость, составляет 3/1 000 000, т. е. 3∙10 -6. Тогда точность определения импульса также составляет 3/1 000 000, или 3∙10 -6измеренной величины, 0,2∙3 кг∙м/сек. Следовательно, Δ( mv ) ~= 2∙10 -6. При этом Δ х∙ Δ( mv ) ~= (5∙10 -7)∙(2∙10 -6) ~= 10 -12. В любом случае нельзя получить это произведение меньшим, чем h = 6,6∙10 -34. В данном примере это произведение получилось в тысячу миллиард миллиардов раз больше его минимальной величины: нет даже намека на подобное ограничение. Просто мы встречаемся с некоторыми экспериментальными трудностями, которые можно преодолеть.

С другой стороны, возьмем электрон, вылетающий из электронной пушки со скоростью 6∙10 6м/сек под действием напряжения 100 в. Попытайтесь сделать так, чтобы диаметр его трека составлял один атомный диаметр, т. е. Δ х ~= 10 -10м, и измерить его скорость с 10 %-ной точностью, т. е. с точностью до 0,6∙10 6м/сек. Тогда

Δ( mv) ~= (масса 9∙10 -31кг)∙(Δ v, 0,6∙10 6м/сек) ~= 5∙10 -25,

Δх∙Δ( mv) ~= 10 -10∙5∙10 -25, или меньше чем, 0,001∙ h.

Здесь наши надежды зашли слишком далеко. Нельзя зафиксировать путь электрона с точностью до одного атомного диаметра и одновременно измерить скорость с точностью, большей 10 %. Это как раз и есть неустранимая неопределенность.

Джон А. Уилер .

NieIs Bohr , Atomic Theory and Description of Nature, Cambridge, 1934.

Построенная, видимо, по предложению Н. Бора для Международной выставки 1939 г. описанная модель представляет собой увеличенную копию модели, сконструированной Воге и Уилером , см. The American Scientist, 44, № 4, October 19563 «A Septet of Sybils», by J. A. Wheeler.

Здесь дается очень упрощенная и не совсем правильная картина рассеяния. На самом деле все обстоит сложнее. В частности, при больших углах рассеяния и больших энергиях вероятность рассеяния увеличивается по сравнению с той, которую следовало бы ожидать при электростатическом взаимодействии частиц. — Прим. ред .

Более легкие мезоны (210 электронных масс), которые были обнаружены первыми, ведут себя несколько иначе, скорее всего как тяжелые нестабильные электроны.

Точное описание прибора см. в статье самого проф. Мюллера , Scientific American, 196, 113, June 1957, в которой приведен целый ряд других снимков и диаграмм.

Можно произвести грубую оценку электрического поля путем следующих рассуждений. Угадаем сначала, каков «радиус» конца иглы. Учитывая, что атомы образуют слои (поглядев на само изображение), догадываемся, что последние слои содержат по меньшей мере дюжину атомов, причем каждый слой лежит на таком же другом, но на один атом шире и т. д. Тогда уже из простого рисунка видно, что радиус острия, выглядящего грубым и «угловатым» в атомном масштабе, равен примерно 30 атомным диаметрам 30 х 3 А° ~= 100∙10 -10м. Атом гелия мал, диаметр его меньше чем 1 А°. Примем его радиус равным 1/ 4А°. Нам известно, что энергия, необходимая для удаления одного электрона, примерно равна 25 эв. Следовательно, для того чтобы оторвать электрон от атома гелия и увести его на бесконечность, необходима разность потенциалов 25 эв, причем большая часть ее должна приходиться на близкие расстояния от атома, где велико поле, создаваемое ядром. Острие вольфрамовой иглы «закруглено», причем радиус закругления в 400 раз больше. Поэтому для создания вокруг него точно такого же поля, как вокруг атома, разность потенциалов между острием и бесконечностью должна быть в 400 раз больше, т. е. должна равняться 400∙25 в, или 10 000 в. Реально между иглой и кольцом прикладывается несколько десятков тысяч вольт. (Большая часть этой разности потенциалов приходится на ближайшую окрестность острия, скажем на расстояние порядка одного радиуса. При этом напряженность поля равна 10 000 в/100∙10 -10м, или 10 12в/м. На расстоянии, равном радиусу атома гелия, это поле дает [10 12в/м]∙[ 1/ 4∙10 -10м], или 25 в, т. е. как раз ту разность потенциалов, которая необходима для ионизации атома. Проведенный расчет, разумеется, представляет собой замаскированный вариант первоначального, но только проведенный в обратном направлении.)