Олег Спиридонов - Людвиг Больцман: Жизнь гения физики и трагедия творца

Первую количественную теорию этого явления создал в 1905 г. А. Эйнштейн. Свой интерес к броуновскому движению он объяснял возможностью проверки справедливости (или ошибочности) молекулярно-кинетической теории. Примечателен подход Эйнштейна к решению задачи. Поскольку все имевшие место до него попытки определения средней скорости движения броуновских частиц были безрезультатны (средняя скорость резко менялась по модулю и направлению, не стремясь к какому-либо пределу при увеличении длительности наблюдений), Эйнштейн выбирает в качестве основной характеристики движения смещение броуновских частиц. Предположив далее, что движение взвешенных частиц полностью хаотично, используя статистику Максвелла — Больцмана, он получил среднее квадратичное смещение частиц вдоль оси x:

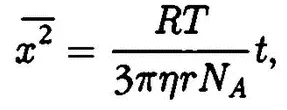
где R — универсальная газовая постоянная, t — время, Т — абсолютная температура, N A— постоянная Авогадро, η — коэффициент вязкости, r — радиус броуновской частицы. Поскольку все величины, входящие в эту формулу, определяются экспериментально, из анализа движения броуновских частиц можно вычислить постоянную Авогадро. Сравнение этого значения N A с данными, полученными из других опытов явилось бы в случае совпадения веским аргументом в пользу справедливости молекулярно-кинетической теории. «Если бы какому-либо исследователю удалось вскоре разрешить поднятые здесь важные для теории теплоты вопросы!» — восклицает Эйнштейн в одной из своих работ.

Прежде всего необходимо было проверить справедливость применения к движению броуновских частиц постулата Эйнштейна о полной хаотичности движения. Идею такой проверки предложил французский физик П. Ланжевен. Для этого надо было расположить в одной точке начало всех смещений броуновских частиц. Если их движение нерегулярно, т. е. подчиняется законам случайности, то концы смещений частиц должны располагаться вокруг их общего центра точно так же, как располагаются при стрельбе вокруг центра мишени попадания пуль. Ж. Перрен выполнил эти исследования. Он проводил в освещенной камере измерения последовательных положений одной и той же броуновской частицы через равные промежутки времени. После 500 измерений он выполнил предлагаемое Ланжевеном геометрическое построение и получил картину, изображенную на рис. 13. Основной постулат Эйнштейна о применимости статистических представлений к анализу движения броуновских частиц получил полное подтверждение. Вслед за этим Перрен и его сотрудники провели вычисления постоянной Авогадро. Рассчитанные ими значения Na совпали со значениями, полученными при использовании других методов, что также подтверждало справедливость теории Эйнштейна. Теперь можно было думать о постановке решающих опытов, называемых experimentum cruris (лат.), доказывающих реальность существования мельчайших структурных единиц материи — молекул и атомов.

Эти опыты выполнили в 1906-1908 гг. Ж. Перрен со своими сотрудниками. Идея опытов проста. Анализируя предположения молекулярно-кинетической теории, Перрен пришел к выводу, что ее результаты применимы не только к молекулам жидкости, но и к броуновским частицам, которые можно рассматривать как большие молекулы. При этом распределение броуновских частиц по высоте должно описываться найденной Больцманом барометрической формулой (13) с заменой в ней массы молекул на массу броуновской частицы. Так как броуновские частицы можно непосредственно наблюдать в микроскоп, изучение их распределения по высоте должно было соответствовать этой формуле, т. е. подтвердить или опровергнуть выводы молекулярно-кинетической теории, дать решающие заключения о реальности существования молекул.

Эксперименты Перрена были весьма трудоемкими и требовали предельной тщательности. Ученый растер в воде желтую краску — гуммигут. Под микроскопом было видно, что в подкрашенной воде находится огромное число желтых шариков различных размеров, твердых и не слипающихся друг с другом. При длительном вращении на центрифуге Перрену удалось отделить порции шариков краски с одинаковыми по размеру зернами. Помещая каплю раствора с зернами гуммигута между двумя горизонтальными стеклами, Перрен наблюдал с помощью микроскопа явное уменьшение взвешенных частиц с высотой, предсказываемое молекулярно-кинетической теорией (см. рис. 8 б). Фокусируя микроскоп на отдельные слои, можно было сфотографировать, а затем подсчитать число частиц в каждом слое. На рис. 14 показаны такие фотографии.

Для выполнения количественных подсчетов Перрен взял четыре слоя, отстоящие друг от друга по вертикали на 5, 35, 65, 95 мкм. Число частиц в слое I, лежащем на высоте h 1, в соответствии с формулой (13) равно

где Е — средняя кинетическая энергия броуновской частицы, P — ее вес. Аналогично для слоя II получим:

Из отношения

нетрудно получить выражение для определения средней кинетической энергии броуновских частиц:

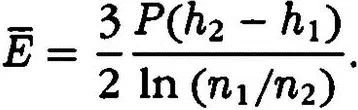
В последнем выражении n 1и n 2определяются экспериментально при непосредственном подсчете числа частиц, разность h 2— h 1 измеряется по сдвигу микрометрического винта микроскопа. Вес броуновских частиц можно определить по формуле

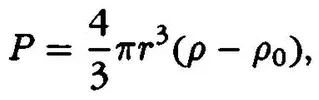
где ρ 0— плотность воды. Радиус частиц r можно получить, измеряя их скорость падения в воде:

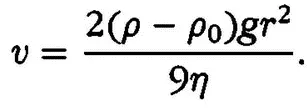
Непосредственно скорость падения отдельных частиц определить нельзя, так как они находятся в хаотическом броуновском движении. Перрен обходит эту трудность следующим способом: эмульсия, налитая в высокий и узкий сосуд, предварительно размешивалась, для того чтобы броуновские частицы распределились в нем равномерно по высоте. Скорость частиц v определялась по скорости оседания границы помутнения. Таким образом были найдены все необходимые для определения г величины, а затем была подсчитана и постоянная Авогадро.