Фрэнк Вильчек - Красота физики. Постигая устройство природы

Это слово используется в математике и физике очень гибко. Оно имеет не одно, а несколько различных точных технических определений в пределах различных областей знаний. Во всех случаях проекция – это отображение одного пространства на другое, с помощью которого информация о первом пространстве представляется в новой форме. Часто (но не всегда) часть информации в этом процессе теряется. В этой книге я использовал слово «проекция» достаточно неформально, без технической скрупулезности, в нескольких тесно связанных смыслах:

• Проекция теней в метафоре Пещеры Платона. Здесь тени создают двумерные бесцветные версии объектов, которые они представляют, и много информации теряется.

• Проекция, которую создают наши глаза, наше зрение. Сетчатка наших глаз получает двумерный образ трехмерного мира. Фокусировка хрусталиком глаза позволяет создавать изображения, в которых (в случае идеального зрения) весь свет, выходящий из некоторой точки рассматриваемого объекта, фокусируется в очень небольшую область на сетчатке, сохраняя таким образом важную пространственную информацию.

Как мы подробно обсуждали в главе «Максвелл II», входной электромагнитный сигнал, который мы называем светом, несет в себе гораздо больше информации, чем извлекают наши глаза.

Человеческое зрение выполняет проекциюбесконечномерного пространства интенсивностей спектральныхцветов на трехмерное пространство воспринимаемого цвета и отбрасывает информацию о поляризации.

• Геометрическая проекция: проекция поверхностей правильных многогранников на описанные вокруг них сферы путем продолжения линий из центра до поверхности; проекция световых лучей на холст в геометрически точном рисовании (вдохновленная живописью наука о перспективе); проекция поверхностей, таких как участки местности или даже вся поверхность Земли, на плоские листы бумаги при создании географических карт.

• Цветоваяпроекция в пространствецветовых свойств. Например, на цветной вклейке X мы спроецировали трехмерное пространство цветовых свойств, координатами которого являются интенсивности R, G, B – красного, зеленого и синего цвета соответственно – на двумерное пространство свойств, просто отбросив одну из координат.

Изучая человеческое восприятие цветов, мы обнаруживаем, что любой воспринимаемый цвет может быть представлен по существу единственным образом – путем смешения трех основных цветов, например, красного, зеленого и синего. Различные интенсивностикрасного, зеленого и синего описываются тремя положительными действительными числами, и каждая такая комбинация интенсивностей соответствует своему особому воспринимаемому цвету. Мы можем интерпретировать эти тройки как координатыв трехмерном пространстве свойств – пространстве воспринимаемых цветов.

Есть много примеров подобного рода, где мы используем числа для обозначения свойств и рассматриваем наборы чисел как координаты, чтобы определить пространство свойств. Пространства свойств, основанные на цветовых зарядах, играют центральную роль в наших Главных теориях.

Протоны наряду с нейтронами являются строительными блоками атомных ядер. Протоны имеют противоположный по отношению к электронам электрический заряди весят примерно в две тысячи раз больше. Большая часть массы обычного веществапоявляется за счет массы протонов и нейтронов, входящих в нее. Раньше думали, что протоны являются элементарными частицами, но сегодня мы знаем, что это сложные объекты, построенные из более элементарных кварков и глюонов.

Уничижительный термин для «Анализа и Синтеза». См. Анализ и Синтез.

Многие металлы и некоторые другие материалы проявляют качественно иное поведение, когда они охлаждены до температуры, близкой к абсолютному нулю. Наиболее существенно то, что их сопротивление протеканию электрического заряда резко падает до нуля. Говорят, что они проявляют сверхпроводимость и становятся сверхпроводниками .

Сверхпроводимость была обнаружена экспериментально Камерлинг-Оннесом в 1911 г. Много лет ее не удавалось объяснить теоретически. Прорыв случился в 1957 г., когда Джон Бардин, Леон Купер и Роберт Шриффер предложили то, что мы теперь называем теорией сверхпроводимости БКШ. Их работа не только объяснила появление сверхпроводимости, но сделала это с использованием очень красивых и мощных идей, которые могли быть – и были – применены к другим задачам. В частности, они предвосхитили спонтанное нарушение симметриии механизм Хиггса.

В сверхпроводниках фотоныведут себя так, будто у них есть ненулевая масса. Уравнения, которые описывают эту ситуацию, по сути такие же, как и уравнения, которые мы используем в Главной теории, чтобы придать ненулевую массу виконамв механизме Хиггса. Я думаю, что будет справедливо и поэтично сказать, что большой урок, который мы можем извлечь из открытия частицы Хиггса, состоит в том, что мы живем внутри космического сверхпроводника. (Но это сверхпроводимость для потока слабого заряда, а не электрического заряда.)

Частицы веществав Главной теории – т. е. кваркии лептоны – имеют одну интересную особенность – трехкратное повторение. Говорят, что они образуют три семейства (по-русски их также называют поколениями ). В каждом семействе насчитывается 16 частиц, образующих схожие структуры из сильных, слабыхи электромагнитных зарядов, которые подробно описываются в основном тексте. Представители трех семейств перечислены в нижеследующей таблице.

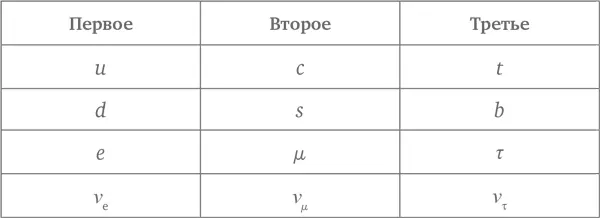
По-другому, пользуясь геометрическим языком главы «Квантовая красота III», мы можем сказать, что каждое из трех семейств содержит шесть сущностей, занимающих в каждом случае одни и те же пространства свойств.

Переходы, связанные со слабым взаимодействием, которые превращают единицу желтого слабого зарядав единицу фиолетового слабого заряда, превращают (левый) u -кварк в (левый) d -кварк, как мы обсудили в основном тексте. Там я ссылался на некоторые сложности и здесь расскажу об этом подробнее. Сложность состоит в том, что переходы слабого цвета могут сопровождаться переходами между семействами . Таким образом, кроме u → d , мы имеем также u → s и u → b. Чтобы описать относительные вероятности таких переходов, необходимо ввести в Главную теориюновые параметры. Угол Кабиббо, например, является мерой того, как соотносятся вероятности второго и первого. Существует множество дополнительных переходов между кварками, которые нужно учесть (например, c → d ), и еще больше, если вспомнить о лептонах. Чтобы описать их все в рамках Главной теории, необходимо ввести около дюжины новых параметров. Величины этих «углов смешивания» были измерены экспериментально, но нет никакой убедительной теории, объясняющей, почему они именно такие.