Леонид Пономарев - По ту сторону кванта

— Позвольте, — возражали ему, — как это — запретить? Между электроном и ядром действуют электрические силы?

— Да, — отвечал Бор.

— Они описываются уравнениями Максвелла?

— Да.

— И даже масса m и заряд е электрона определены из электрических измерений?.

— Да.

— Значит, движение электрона в атоме также должно подчиняться электродинамике Максвелла?

— Нет!

Согласитесь, что такой способ ведения спора может рассердить даже очень спокойного человека. «Но ведь атом все-таки устойчив! — без конца повторял Бор в ответ на все возражения. — И мы не знаем более простой причины этой устойчивости, кроме той, что она есть».

В поисках разумного основания для этого несомненного факта Бор наткнулся на книгу Иоганна Штарка «Принципы атомной динамики» и там впервые увидел формулы Бальмера и Ридберга.

«Мне сразу все стало ясно, — вспоминает Бор. — И после многочисленных попыток использовать квантовые идеи в более строгой форме ранней весной 1913 года мне пришло в голову, что ключом к решению проблемы атомной устойчивости являются изумительно простые законы, определяющие оптический спектр элементов».

Теперь он мог сформулировать свои знаменитые постулаты:

1-й постулат — о стационарных состояниях. В атоме существуют орбиты, вращаясь по которым электрон не излучает.

2-й постулат — о квантовых скачках. Излучение происходит только при перескоке электрона с одной стационарной орбиты на другую. При этом частота излучения ν определяется гипотезой Эйнштейна о квантах света ΔЕ — hν, где ΔЕ — разность энергий уровней, между которыми происходит переход.

Чтобы понять эти постулаты несколько глубже, обратимся к очевидной аналогии между предполагаемым вращением электрона вокруг ядра и вращением спутника вокруг Земли. В свое время Ньютон открыл закон всемирного тяготения, размышляя над вопросом: «Почему Луна не падает на Землю?» Сейчас этот вопрос задают только в старых анекдотах, ибо все знают ответ: «Потому что она движется, причем со строго определенной скоростью, которая зависит от расстояния ее до Земли». Таким образом, чтобы спутник не упал на Землю и в то же время не улетел в космос, между радиусом его орбиты r и скоростью движения по ней v должна существовать определенная связь.

В атоме водорода при движении электрона с массой m и зарядом е вокруг ядра атома между скоростью электрона v на орбите и радиусом орбиты r существует аналогичная связь, которую можно записать в виде уравнения: (m v 2/2) = (e 2/r 2).

Это уравнение верно всегда — независимо от того, излучает электрон или не излучает. Оно просто отражает известное равенство центростремительной и притягивающей сил.

Если электрон теряет энергию на излучение (по законам электродинамики), то он упадет на ядро, как спутник при торможении в атмосфере. Но если существуют особые — стационарные — орбиты, на которых он не подчиняется законам электродинамики и потому не излучает, то должны существовать также дополнительные условия, которые выделяют эти орбиты из набора всех возможных.

Как появляются эти условия, легче всего показать, продолжив нашу аналогию со спутником.

У кругового движения, кроме радиуса орбиты r и скорости v движения по ней, есть еще одна характеристика — момент количества движения l, или, коротко, орбитальный момент l . Он равен произведению массы m на скорость v и на радиус орбиты r, то есть l = m v r, и для спутника может принимать произвольные значения в зависимости от величины r и v.

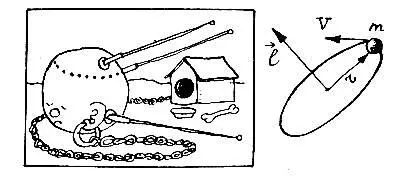
Бор утверждал: электрон в атоме отличается от спутника тем, что его орбитальный момент l не может быть произвольным. — он равен целому кратному от величины ħ = h/2π (это обозначение предложил один из создателей квантовой механики, Поль Дирак)

mvr = n ħ.

Это и есть то дополнительное условие Бора, которое выделяет стационарные орбиты (единственно допустимые в атоме) из бесконечного числа мыслимых. А поскольку при таком выделении основную роль играет квант действия h, то и весь процесс назвали квантованием.

Из предыдущих двух условий Бор легко получил значения энергии Е nрадиусов r nстационарных орбит:

r n= (ħ 2)/(m e 2) n 2; Е n= [-(m e 4)/(2 ħ 2)] • (1/n 2).

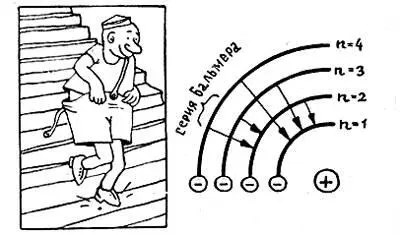
Стационарные орбиты (а следовательно, и уровни энергии) нумеруются целыми числами n или k, которые пробегают бесконечный ряд значений: 1, 2, 3… При переходе с уровня n на уровень k электрон излучает энергию ΔЕ = Е k— Е n, а частота излучения, которое при этом возникает, определяется по формуле Эйнштейна;

ν = ΔЕ/h = (Е k— Е n)/(2πħ)

Если мы наблюдаем излучение, которое возникает при переходах электрона со всевозможных уровней k на какой-то определенный уровень п, то мы увидим не просто набор спектральных линий, а серию . Например, если n = 2, а k = 3, 4, 5, 6… то мы увидим серию Бальмера. Отсюда сразу же следует знаменитая формула Бора для частоты излучения атома водорода:

ν = [(me 4)/(4πħ 3)] (1/n 2-1/k 2).

Что из нее следует?

Прежде всего она очень напоминает формулу Ридберга для атома водорода, которую тот нашел эмпирически задолго до Бора и о которой мы подробно рассказали в предыдущей главе. Если формула Бора верна, то из нее можно вычислить постоянную Ридберга R.

R = (me 4)/(4 πcħ 3).

Вычислили. И действительно, ее значение совпало с тем, которое давно было известно из спектроскопических измерений.

Это был первый успех теории Бора, и он произвел впечатление чуда.

Но это еще не все. Из теории Бора следовало, что радиус атома водорода в основном (невозбужденном) состоянии (n=1) равен

r 1= ħ 2/me 2= 0,53 10 -8см = 0,53 Ǻ

Это означает, что размеры атомов (≈ 10 -8см), вычисленные по его формуле, совпадали с предсказаниями кинетической теории материи.

И наконец, теория Бора объяснила: как свойства линейчатого спектра связаны с внутренним строением атома. Интуитивно эту связь чувствовали всегда. Но только Бору впервые удалось выразить ее математически. Оказалось, что искомую связь осуществляет постоянная Планка h.

Это было неожиданно. Действительно, квант действия h возник в теории теплового излучения и никаким очевидным образом не был связан ни с атомами, ни с лучами, которые эти атомы испускают. И тем не менее именно он позволил вычислить абсолютные размеры атома и предсказать частоту света, излучаемого им. Угадать эту связь Бору, как и многим до него, помогла глубокая вера в единство природы.

Постулаты Бора (как и всякие постулаты) нельзя обосновывать логически или вывести из более простых. Они остаются произвольными творениями человеческого разума до тех пор, пока опыт не подтвердит следствий, которые из них вытекают. Тогда на их основе развиваются теории, а наиболее удачные из теорий называют законами природы.