Брайан Грин - Ткань космоса. Пространство, время и текстура реальности

Возможность того, то мы живём внутри 3-браны (так называемый сценарий мира на бране ), является самым последним поворотом теории струн / M-теории. Как мы увидим, она открывает совершенно новый взгляд на теорию струн / M-теорию с многочисленными и далеко идущими последствиями. Суть дела в том, что браны во многом подобны космической «липучке»; определённым образом, который мы сейчас обсудим, они очень липкие.

Один из мотивов введения термина «M-теория» состоит в том, что, как мы теперь видим, название «теория струн» подчёркивает лишь один из множества объектов теории. Одномерные струны были обнаружены в теоретических исследованиях за десятилетия до того, как более тонкий анализ обнаружил существование бран более высокой размерности, так что «теория струн» — в чём-то устаревшее название. Однако, хотя M-теория и устанавливает своего рода «демократию» среди многообразия объектов различной размерности, но струны всё же играют главную роль в нашей современной формулировке. Одна из причин сразу же ясна. Можно игнорировать все p -браны более высокой размерности в ситуации, когда они гораздо тяжелее струн, — так исследователи неосознанно и поступали с 1970-х гг. Но есть и ещё одна причина, носящая более общий характер и делающая струны «первыми среди равных».

В 1995 г., вскоре после того как Виттен объявил о своём открытии, Джозеф Польчински из Калифорнийского университета в Санта-Барбаре получил богатую пищу для размышлений. Несколькими годами ранее в статье, написанной совместно с Робертом Леем и Джином Даем, Польчински обнародовал интересное и загадочное свойство теории струн. Мотивировки и рассуждения Польчински были несколько техническими, но детали для нас не важны, а результаты таковы. Он обнаружил, что в определённых ситуациях концы открытых струн (напомним, что такие струны представляют собой отрезки с двумя свободными концами) не могут двигаться как им угодно. Подобно тому как бусинка на проволочке может свободно двигаться, но при своём движении вынуждена повторять контур проволоки, и подобно тому как пинбольный шарик свободен в своём движении, но должен повторять контуры поверхности пинбольного стола, так и концы незамкнутой струны могут свободно двигаться, но ограничены в своём движении определёнными формами или контурами в пространстве. Польчински с соавторами показал, что хотя струна всё ещё вольна колебаться, но её концы будут «приклеены» к определённым областям или «захвачены» ими.

В одних ситуациях эта область может быть одномерной, и тогда концы струны уподобляются двум бусинкам, скользящим по проволоке, а сама струна — ниточке, связывающей их. В других ситуациях эта область может быть двумерной, и тогда концы струны уподобляются двум пинбольным мячам, связанным одной нитью и катающимся по пинбольному столу. Ещё в других ситуациях область может иметь три, четыре или любое число пространственных измерений не выше девяти. Эти результаты, как показал Польчински, а также Пётр Хоржава и Майкл Грин, помогли решить давнюю загадку, возникающую при сравнении замкнутых и незамкнутых струн, но в течение ряда лет эта работа привлекала мало внимания. {176} Всё изменилось в октябре 1995 г., когда Польчински закончил пересмотр этих ранних результатов в свете новых открытий Виттена.

Работа Польчински оставляла без ответа следующий вопрос, который, возможно, возник у вас при чтении предыдущего абзаца: если концы незамкнутых струн удерживаются внутри определённой области пространства, то к чему же они приклеены ? Проволока и пинбольный стол существуют сами по себе, независимо от бусинок или шариков, движение которых они ограничивают. Что это за области пространства, к которым привязаны концы незамкнутых струн? Заполнены ли они неким независимым и фундаментальным ингредиентом теории струн, который так ревностно удерживает концы незамкнутой струны? До 1995 г., когда единственными объектами теории струн были только струны, не виделось подходящего кандидата на эту роль. Но после открытия Виттена и шквала последовавших работ ответ стал очевиден Польчински: если концы незамкнутых струн обязаны находиться внутри некой p -мерной области пространства, то эта область должна заниматься p -браной [81]. Его расчёты показали, что вновь открытые p -браны в точности обладают свойствами объектов, неумолимо захватывающих концы открытых струн, вынуждая их двигаться в пределах p -мерной области пространства, занимаемой браной.

Чтобы получить более ясное представление, взглянем на рис. 13.2. На рис. 13.2 а мы видим пару 2-бран с массой движущихся колеблющихся струн, концы которых ограничены в своём движении этими бранами. Ситуация с бранами более высокой размерности совершенно идентична, хотя её труднее изобразить. Концы открытых струн могут свободно двигаться по p -бранам и внутри них, но они не могут покинуть саму брану. Когда речь заходит о возможности движения вне браны, то браны оборачиваются самой клейкой вещью, какую только себе можно представить. Возможно также, что один конец открытой струны захвачен одной p -браной, а другой конец — другой p -браной, которая может иметь либо ту же самую размерность, что и первая (рис. 13.2 б ), либо другую (рис. 13.2 в ).

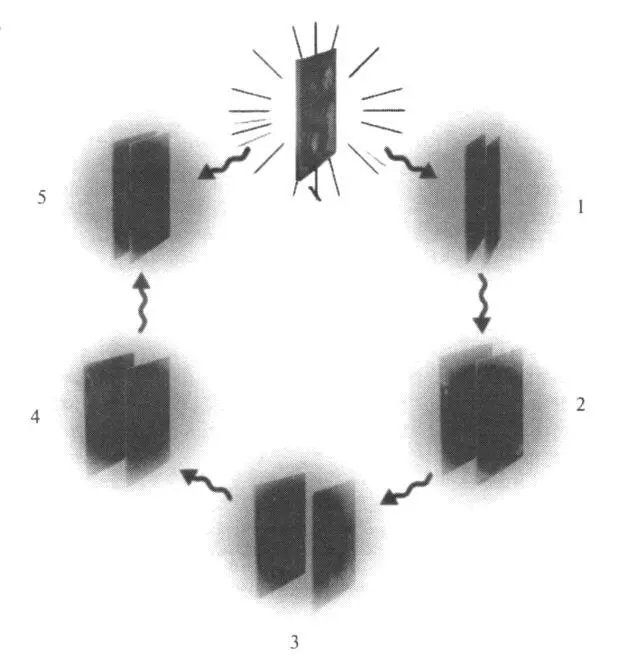
Рис. 13.2.( а ) Открытые струны, с концами, прикреплёнными к двумерным бранам (2-бранам). ( б ) Струны, соединяющие две разные 2-браны. ( в ) Струны, соединяющие 2-брану и 1-брану

Работа Польчински как нельзя кстати подошла к открытию Виттена, вызвавшему вторую революцию в теории суперструн. В то время как некоторые из величайших умов в теоретической физике XX в. тщетно пытались сформулировать теорию, содержащую фундаментальные объекты с бо́льшим числом измерений, чем точки (нульмерные) или струны (одномерные), результаты Виттена и Польчински, дополненные важными достижениями множества современных ведущих исследователей, открыли путь к прогрессу в этом направлении. Эти физики не только установили, что теория струн / M-теория содержит объекты более высокой размерности, но результаты Польчински, в частности, дали средства для теоретического анализа их детальных физических свойств (если будет доказано их существование). Польчински показал, что свойства браны определяются в значительной степени свойствами открытых колеблющихся струн, концы которых она захватывает. Подобно тому как вы многое можете узнать о ковре, проведя рукой по его ворсу — шерстяным нитям, прикреплённым к подложке ковра, — так и многие свойства браны можно выяснить, изучая струны, концы которых она держит.