Брайан Грин - Ткань космоса. Пространство, время и текстура реальности

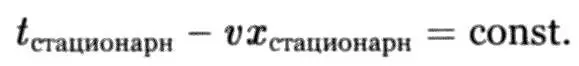
Такие срезы наклонены под некоторым углом к временны́м слоям стационарного наблюдателя ( t стационарн= const), а поскольку υ < 1, то угол между ними не может превосходить 45°.

Для математически подкованного читателя это утверждение можно строго сформулировать следующим образом: геодезические линии пространства-времени Минковского (пути экстремальной длины между двумя точками пространства-времени) являются геометрическим объектами, не зависящими от выбора координат или системы отсчёта. Эти линии являются внутренними, абсолютными геометрическими свойствами пространства-времени. Точнее говоря, в стандартной метрике Минковского геодезические (времениподобные) линии являются прямыми (составляющими с осью времени угол меньше 45°, поскольку скорость материального объекта не может превышать скорость света).

Есть ещё кое-что важное, с чем согласятся все наблюдатели, независимо от скорости их движения. Это подразумевается в нашем описании пространства-времени, но стоит сказать об этом прямо! Если одно событие является причиной другого (я кинул камень в окно, и окно разбилось), то все наблюдатели согласятся с тем, что причина стояла перед следствием (все согласятся, что я кинул камень перед тем, как окно разбилось). Для математически подкованного читателя это нетрудно показать с помощью нашего схематического описания пространства-времени. Если событие A является причиной события B , то линия, проведённая в пространстве-времени от A до B пересечёт каждый временно́й слой (временно́й слой наблюдателя, покоящегося по отношению к A ) под углом, превышающим 45°. Например, если события A и B произошли в одном и том же месте пространства (от резинки, натянутой вокруг моего пальца [событие A ] мой палец побелел [событие B ]), то линия, соединяющая A и B , перпендикулярна плоскостям временны́х слоёв (составляет с ними угол 90°). Если же события A и B произошли в разных точках пространства (камень летит в окно), то всё же влияние из A в B передавалось со скоростью, не превышающей скорость света, откуда следует, что соответствующая траектория в пространстве-времени не может отклониться от оси времени на угол, превышающий 45°, и, значит, угол между траекторией и любым временны́м слоем всегда больше 45°. (Вспомните из примечания 9, что только свет может отклоняться на максимальный угол 45° по отношению к оси времени.) Временны́е слои двигающегося наблюдателя наклонены под углом к временны́м слоям неподвижного наблюдателя, но этот угол наклона всегда меньше 45° (поскольку относительная скорость движения двух наблюдателей не может превышать скорость света). И, поскольку угол траектории, связанной с причинно связанными событиями, всегда больше 45°, то эта траектория не может пересечь временно́й слой, относящийся к следствию, раньше слоя, относящегося к причине. Поэтому для всех наблюдателей причина всегда предшествует следствию.

Кроме того, если влияние могло бы распространяться быстрее света, это нарушало бы причинность.

Newton I. Sir. Isaac Newton’s Mathematical Principles of Natural Philosophy and His System of the World. P. 634.

Поскольку гравитационное притяжение Земли меняется от точки к точке, то свободно падающий наблюдатель (имеющий ненулевые размеры) всё же может обнаружить остаточное воздействие гравитационной силы. А именно, если этот наблюдатель выпустит по бейсбольному мячу из двух своих вытянутых в стороны рук, то каждый из мячей полетит по своей траектории к центру Земли. Поэтому с точки зрения этого наблюдателя он сам будет падать строго вниз к центру Земли, тогда как мяч, выпущенный из правой руки, будет падать с еле заметным отклонением влево, а мяч, выпущенный из левой руки, будет падать с едва заметным отклонением вправо. Проводя тщательные замеры, наблюдатель заметит, что расстояние между мячами мало-помалу сокращается; они двигаются навстречу друг другу. Здесь важно то, что мячи были выпущены в разных, хотя и близких, точках пространства, поэтому их траектории свободного падения по направлению к центру Земли, хотя и почти незаметно, но отличаются. Таким образом, более точное утверждение, отражающее догадку Эйнштейна, состоит в том, что чем меньше размеры объекта, тем полнее он может устранить гравитацию в своём свободном падении. Но в нашем обсуждении этим обстоятельством можно благополучно пренебречь, хотя оно и важно в принципе.

Для математически подготовленного читателя приведём уравнения Эйнштейна: G μν = (8 πG / c 4) T μν , где в левой части стоит тензор Эйнштейна, описывающий кривизну пространства-времени, а в правой части — тензор энергии-импульса T μν , описывающий распределение материи и энергии во Вселенной.

Мизнер Ч., Торн К., Уилер Дж. Гравитация. Т. 2. М.: Мир, 1977. С. 192–195.

В 1954 г. Эйнштейн писал коллеге: «Кстати, о принципе Маха вообще больше говорить не стоит» (цитируется по книге: Пайс А. Научная деятельность и жизнь Альберта Эйнштейна. С. 279).

Как отмечалось ранее, следующие идеи были впоследствии приписаны Маху, хотя он сам никогда не выражал их столь буквально.

С той оговоркой, что объекты, настолько удалённые от нас, что с момента рождения Вселенной их свет или гравитационное воздействие ещё нас не достигли, не влияют на ощущаемую нами гравитацию.

Искушённый читатель заметит, что, формально говоря, это слишком сильное утверждение, поскольку для пустого пространства имеются нетривиальные решения общей теории относительности (т. е. такие, которые дают не пространство Минковского, а нечто более сложное). Здесь я просто использую тот факт, что специальная теория относительности может рассматриваться как специальный случай общей теории относительности, если не учитывать гравитацию.

Строго говоря, не все физики и философы согласны с этим заключением. Хотя Эйнштейн отказался от принципа Маха, в течение последних тридцати лет этот принцип вёл собственную жизнь. Выдвигались различные версии и интерпретации идей Маха. Так, например, некоторые физики предполагали, что общая теория относительности в своей основе охватывает идеи Маха, и только некоторые особые формы, которые может иметь пространство-время, — такие как бесконечное плоское пространство-время в пустой Вселенной, — не отвечают принципу Маха. Возможно, предполагали они, любое пространство-время, которое хотя бы отдалённо реалистично (населено звёздами и галактиками и т. д.), удовлетворяет принципу Маха. Другие предлагали новые формулировки принципа Маха, в которых дело было больше не в том, как объекты, подобные связанным верёвкой камням или наполненному водой ведру, ведут себя Вселенной, а скорее в том, как различные временные слои — различные геометрии трёхмерного пространства — связаны друг с другом во времени. Поучительные ссылки на современное осмысление этих идей содержатся в книге Mach’s Principle: From Newton’s Bucket to Quantum Gravity (Julian Barbour and Herbert Pfister, eds. Berlin: Birkhäuser, 1995), являющейся сборником статей по данной теме. В этой книге содержится также опрос примерно сорока физиков и философов по поводу их взгляда на принцип Маха. Большинство (90%) согласны, что общая теория относительности не полностью согласуется с идеями Маха. Другое чрезвычайно интересное обсуждение этих идей с точки зрения, поддерживающей идеи Маха, и на уровне, доступном широкому читателю, содержится в книге: Barbour J. The End of Time: The Next Revolution in Physics. (Oxford: Oxford University Press, 1999).