Валерий Асадов - Физика (Третья) 21 века. Том 1

И если мы возьмем формулу плотности p=M/V, подставим туда радиус черный дыры в объем, то получим первую космологическую формулу (соотношение).

Что самое интересное, что плотность Вселенной зависит только от одной величины, от масс Вселенной и не зависит от объема и радиуса. А если в эту формулу подставить

(21), то получим второе космологическое соотношение, где плотность, где плотность зависит только от радиуса Вселенной.

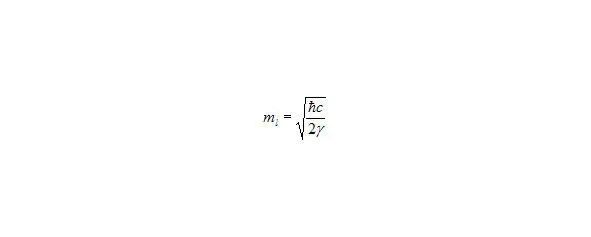
Рис.9. Формула 21. Масса планкеона. Привлеченная.

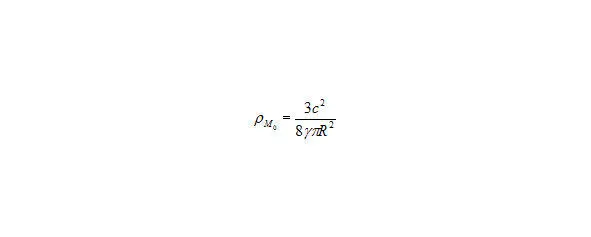
Рис. 10. Второе космологическое соотношение, где плотность Вселенной зависит от радиуса Вселенной.

Дальше подставляем вместо радиуса скорость, умноженную на время,

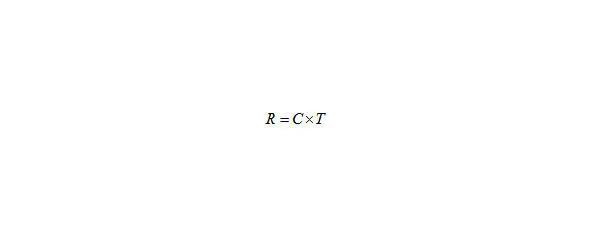
Рис. 11. Дальше подставляем вместо радиуса скорость, умноженную на время,

то получим третье космологическое соотношение через время, где плотность Вселенной зависит только от возраста Вселенной.

Плотность Вселенной, выраженной через постоянную Хаббла, получим если в

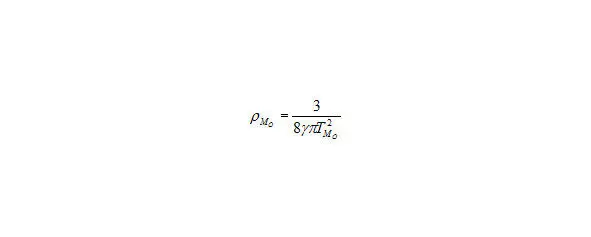
Рис. 12. Третье космологическое соотношение. Плотность Вселенной через возраст Вселенной.

формулу (5). Подставим вместо времени постоянную Хаббла – T=1/H формула (23):

Плотность Вселенной, выраженную через постоянную Хаббла.

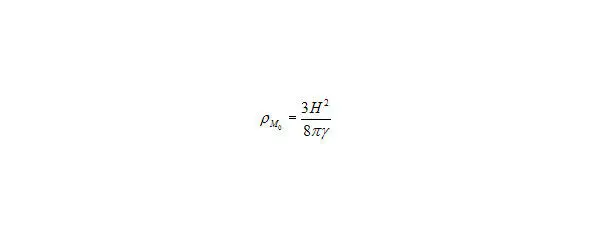
Рис. 13. Плотность Вселенной выраженную через постоянную Хаббла, или иначе критическая плотность Вселенной.

И что интересное эта формула абсолютна идентична формуле критической плотности Вселенной полученный совершенно другим путем. Формула (другая) критической плотности Вселенной

Приведу вывод этой формулы в современной физике, для того чтобы Вам была ясна и понятна, разница в методике подхода и мышления современной физики и Н. Д. В. Ф. Из книги Новикова. И.Д. «Эволюция Вселенной»

«Несложно определить это критическое значение плотности. Действительно, известно, что вторая космическая скорость для шара массой М записывается следующем способом: v=√2*g*M/R.

(13)

Подставляя в (13) выражения для массы M=ρ*4/3*π*R 3, а вместо скорости v=H*R, находим H*R=√ (8*g*π/3) *ρR 2, или, выражая отсюда плотность ρ,

(14)

Итак, критическое значение средний плотности во Вселенной зависит от постоянной Хаббла Н. При постоянной Хаббла Н=75 кмсек*Мпс, для критической плотности получаем ρ=10 г/см*10 —29» 1 1 Из книги «Эволюция Вселенной», автор Новиков И. Д., Москва, «Наука», 1983 г., стр. 36—38.

Аналгичной той формулы, которую мы получили в динамической физики. Вселенная это «черная дыра». И начнем активно применять эту формулу. Привожу цитату, для невольного подтверждение мыслей автора:

«Радиус Шварцшильда сферы, равномерно заполненной веществом с плотностью, которая равна критической плотности, совпадает с радиусом наблюдаемой Вселенной» 2 2 Цитата из «Wikia».

Если в формулу Ньютона F=m*a (43) подставим m→Mo, а вместо F→Flim придел силы, вместо

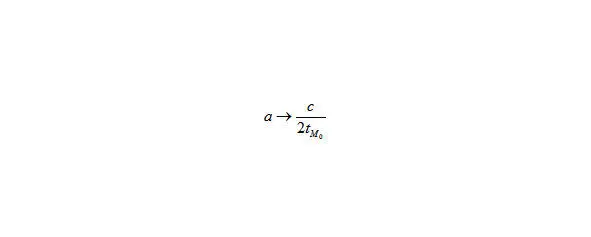
Рис. 14. Скорость света, деленную на удвоенный возраст Вселенный. Привлеченная.

(24) скорость света, деленную на удвоенный возраст Вселенный. То получим формулу Силовое соотношение (17).

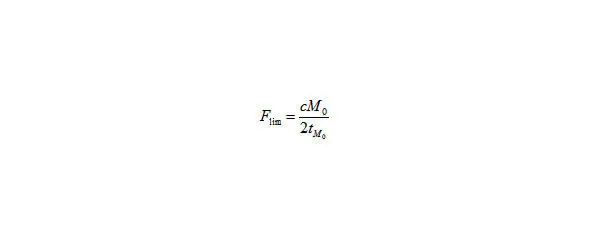
Рис. 15. Формула Силового соотношения (17).

Возьмем предел силы из статьи «Предел силы» (18)

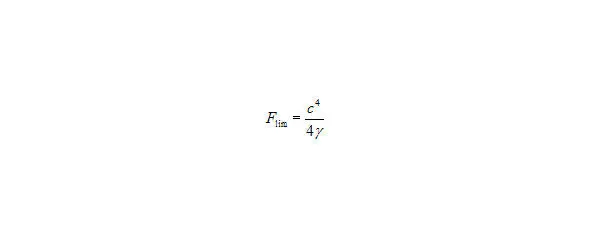
Рис. 16. Формула Предела силы (18)

и соединим эти две формулы в одну – (20),

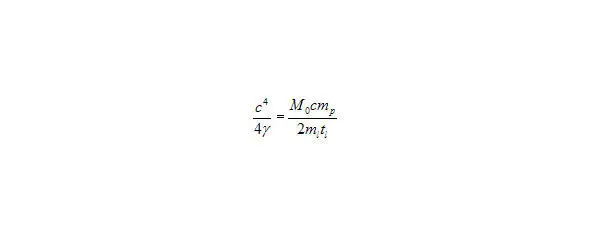
Рис. 17. Формула 20.

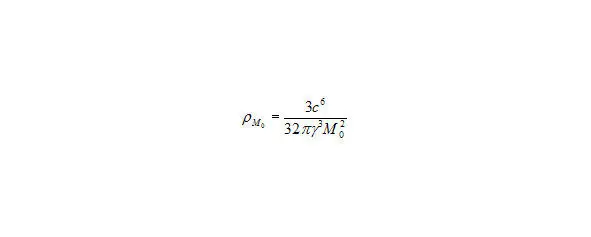
Рис. 18. Первое космологическое соотношение. формулу (3)

а также возьмем формулу (3),

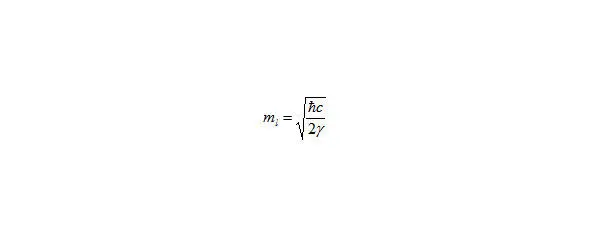
Рис. 19. формулу планкеона (21). Привлеченная.

и формулу планкеона (21).

Соединим и подставим, то получим формулу (10).

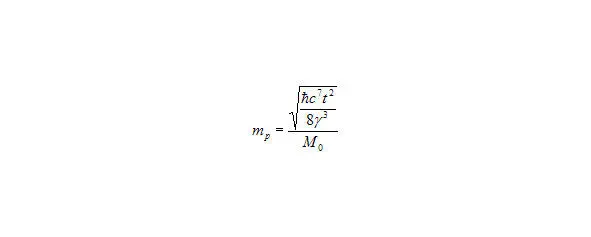
Рис. 20. формулу (10).

Где, как и говорилось, что масса Вселенной зависит от массы протона, чем больше уменьшается масса протона, тем больше увеличивается масса Вселенной. Если использовать мысль Дирака о том, что количество протонов N=Mo/Mp (18) то получим. То есть, зная массу протона в нужном нам времени возраста Вселенной, мы всегда можем вычислить количество протонов во всей нашей Вселенной в это нужное нам время. Если возьмем формулу Ньютона

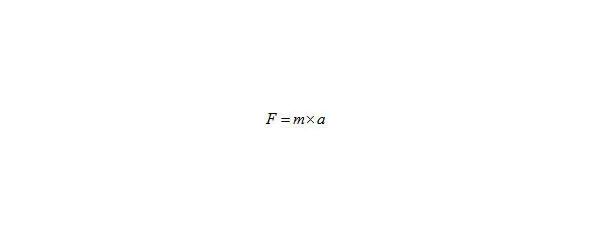
Рис. 21. формулу Ньютона.

Рис. 22.

и формулы (13), (), то получим формулу абсолютного ускорения (15).

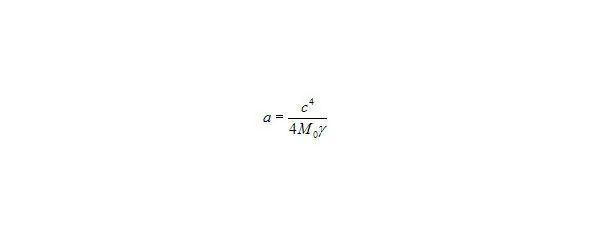
Рис. 23. формулу абсолютного ускорения (15).

А если вместо массы подставим первое космологическое соотношение (3),

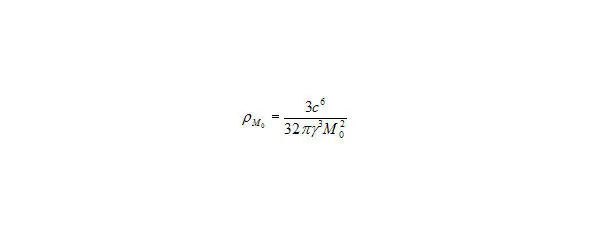
Рис. 24. первое космологическое соотношение (3),