Нурбей Гулиа - Физика: Парадоксальная механика в вопросах и ответах

Автор предлагает пользоваться таким приемом: если можно достать вытянутой рукой до верхней ступеньки лестницы, то нужно потянуть за нее вниз – если лестница не падает, то на нее можно забираться. Если верхняя ступенька высоко, то к ней можно привязать веревку и тянуть за нее вниз.

4.4. Вопрос. Чем была сила в понимании древних людей?

Ответ. Древние люди различали два вида движения – естественное и насильственное. В нашем понимании естественное движение – это движение инерционное, без приложения внешних сил. Летит себе астероид в космическом пространстве с постоянной скоростью и по прямой – это и есть его естественное движение.

Но древние под естественным движением имели в виду нечто другое – возвращение предмета на его «естественное» место: если это камень, то вниз, если огонь, то наверх, на небо. И чтобы изменить это естественное движение, нужно было приложить силу – поднять камень вверх и т. д.

Из древних ученых наиболее серьезно занимался вопросами движения и сил Аристотель. Интересно, что древних греков совершенно не интересовало направление движения – им были важны только начальная и конечная точки движения.

Сила, названная Аристотелем «динамис», могла быть в современных обозначениях записана так:

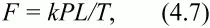
где Р – вес движимого тела,

L – длина пути,

Т– время движения,

k – безразмерный коэффициент пропорциональности, видимо, имевший что-то общее с коэффициентом трения.

Поэтому размерностью аристотелевой силы по современным понятиям будет Н?м/с, т. е. Вт – единица мощности.

Даже из рассуждений Аристотеля можно было сделать вывод, что под силой он подразумевал мощность. Он считал, что одной и той же силой можно продвинуть половинный груз на вдвое большее расстояние, или на то же расстояние в половину времени. Видно, что сила отождествлена с работой и мощностью.

Сущность Аристотелевой силы подтверждается и терминологией. Греческое «динамис» переводится латинским «potentia», что соответствует французскому «puissance», или русскому «мощность». Античное воззрение на силу отразилось и на существующей до сих пор единице мощности – лошадиной силе. В действительности же лошадиная сила – это не сила, а работа эталонной лошади, отнесенная ко времени, в течение которого эта работа была совершена, то есть мощность. И возникла эта единица как количественная оценка паровой машины Уатта по мощности, а не по силе, которая в этом случае не имеет никакого смысла.

4.5. Вопрос. В законе всемирного тяготения массы считаются точечными. А в действительности они огромны по размерам, например наша Земля. Как будет действовать этот закон внутри нашей планеты?

Ответ. При ответе на этот вопрос мы столкнемся с рядом трудностей. Если тело находится на большой высоте над Землей, к тому же в безвоздушном пространстве, то силу притяжения этого тела к Земле можно определить по закону всемирного тяготения, а зная массу этого тела – ускорение по второму закону Ньютона. Подставив силу F притяжения двух тел – Земли и падающего тела – из закона всемирного тяготения:

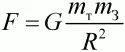
в формулу второго закона Ньютона F = тTа и разрешив полученное выражение относительно ускорения, получим:

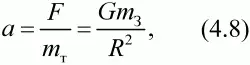
где G – гравитационная постоянная;

тЗ и тT – соответственно, массы Земли и тела;

R – расстояние между центрами масс тела и Земли.

Заметим, что ускорение а не зависит от массы самого тела.

При попадании в атмосферу Земли картина притяжения тела Землей меняется (здесь, конечно же, не идет речи об аэродинамическом сопротивлении атмосферы движению тела). С одной стороны, центр тяжести Земли становится ближе, и сила притяжения увеличивается. Вместе с тем, тело начинают притягивать массы воздуха, расположенные с другой стороны от центра масс Земли. Ускорение уже нельзя определить по формуле (4.8).

Далее, пусть тело достигнет уровня океана. Здесь перед нами встает новый вопрос: считаем ли мы, что рассматриваемое тело вращается вместе с Землей или оно неподвижно относительно «абсолютной» системы отсчета?

Если тело находится на полюсе, безразлично, на Северном или Южном, ускорение свободного падения g = 9,83 м/с2. Вращение Земли тут роли не играет: полюс – это неподвижная точка относительно инерциальной системы отсчета, если не принимать в расчет вращения Земли вокруг центра масс Солнечной системы, прецессии земной оси и других факторов, мало влияющих на отклонения движения полюса от инерционного. Но Земля «сплюснута» у полюсов и «раздута» у экватора из-за своего суточного вращения. Поэтому на полюсе тело максимально приближено к центру Земли.

На экваторе же из-за отдаленности от центра, а еще более – из-за вращения Земли, которое теперь уже мы не можем игнорировать (невозможно представить себе тело, находящееся на Земле, а тем более заглубленное в нее, и не вращающееся вместе с ней!), ускорение свободного падения g = 9,78 м/с2.

Далее, величина ускорения свободного падения зависит от того, над чем находится тело: над глубоким океаном, где плотность воды невелика – около 1000 кг/м3, или над сушей, где плотность доходит до 2600 кг/м3и более (например, над залежами железной руды), или над пустотами, если даже они заполнены нефтью или газом. Ускорение свободного падения тем больше, чем плотнее материал под телом, и тем меньше, чем он менее плотен.

Положение усложняется, когда мы начинаем заглублять рассматриваемое тело в Землю. Если мы опускаем его на дно океана, то над телом оказывается легкая вода. Она хоть и притягивает тело в сторону от центра масс Земли, но этот центр, оказываясь все ближе, доминирует в притяжении. Если мы заглубляем тело в грунт, скальные породы или железнорудные залежи, то притяжение от центра все существеннее.

Следует иметь в виду, что плотность вещества в центре Земли очень высока – около 12000 кг/м3– это побольше, чем у свинца! Поэтому величина ускорения свободного падения g еще достаточно долго при заглублении в Землю увеличивается. Но потом она неизбежно начинает уменьшаться и в центре масс Земли ускорение свободного падения равно нулю. Тело одинаково притягивается внешними слоями Земли.

Интересно, что было бы, если бы Земля была полой и вся ее масса была сосредоточена в оболочке? Тогда, оказавшись в полости, все предметы «плавали» бы в ней, находясь в невесомости, как в космическом корабле!