Иосиф Шкловский - Звезды: их рождение, жизнь и смерть

При температуре порядка десяти миллионов кельвинов и при плотностях, которые там существуют, все атомы должны быть ионизованы. В самом деле, средняя кинетическая энергия каждой частицы газа 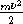= 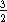kT будет около 10 -9эрг или 1000 эВ.

Это означает, что каждое столкновение электрона с атомом может привести к ионизации последнего, так как энергия связи электронов в атоме (так называемый «потенциал ионизации»), как правило, меньше тысячи электронвольт. Только самые «глубокие» электронные оболочки у тяжелых атомов останутся «нетронутыми», т. е. будут удержаны своими атомами. Состояние ионизации внутри-звездного вещества определяет его среднюю молекулярную массу, величина которой, как мы уже имели возможность убедиться, играет большую роль в недрах звезд. Если бы вещество звезды состояло только из полностью ионизованного водорода (как мы положили выше), то средняя молекулярная масса 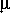, равнялась бы 1 / 2. Если бы там был только полностью ионизованный гелий, то 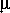= 4 / 3 (так как при ионизации одного атома гелия с атомной массой 4 образуются три частицы — ядро гелия плюс два электрона). Наконец, если бы вещество недр звезды состояло только из тяжелых элементов (кислорода, углерода, железа и пр.), то средняя молекулярная масса его при полной ионизации всех атомов была бы близка к 2, так как для таких элементов атомная масса приблизительно вдвое больше, чем число электронов в атоме.

В действительности вещество звездных недр представляет собой некоторую смесь водорода, гелия и тяжелых элементов. Относительное содержание этих основных компонент звездного вещества (не по числу атомов, а по массе) обычно обозначается через буквы X , Y и Z , которые характеризуют химический состав звезды. У типичных звезд, более или менее сходных с Солнцем, X = 0 , 73, Y = 0 , 25, Z = 0 , 02. Отношение Y/X 0 , 3 означает, что на каждые 10 атомов водорода приходится приблизительно один атом гелия. Относительное количество тяжелых элементов весьма мало. Например, атомов кислорода примерно в тысячу раз меньше, чем водорода. Тем не менее роль тяжелых элементов в структуре внутренних областей звезд довольно значительна, так как они сильно влияют на непрозрачность звездного вещества. Среднюю молекулярную массу звезды мы можем теперь определить простой формулой:

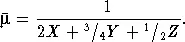(6.3)

Роль Z в оценке 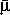незначительна. Решающее значение для величины средней молекулярной массы имеют X и Y . Для звезд центральной части главной последовательности (в частности, для Солнца) 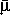= 0 , 6. Так как величина 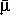для большинства звезд меняется в очень незначительных пределах, мы можем написать простую формулу для центральных температур различных звезд, выразив их массы и радиусы в долях солнечной массы M и солнечного радиуса R :

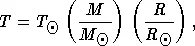(6.4)

где T — температура центральных областей Солнца. Выше, мы грубо оценили T в 10 миллионов кельвинов. Точные вычисления дают значение T = 14 миллионов кельвинов. Из формулы (6.4) следует, например, что температура недр массивных горячих (на поверхности!) звезд спектрального класса В раза в 2—3 выше температуры солнечных недр, в то время как у красных карликов центральные температуры раза в 2—3 ниже солнечных.

Существенно, что температура 10 7К характерна не только для самых центральных областей звезд, но и для окружающего центр звезды большого объема. Учитывая, что плотность звездного вещества растет по направлению к центру, мы можем сделать вывод, что основная часть массы звезды имеет температуру, во всяком случае превышающую 5 миллионов кельвинов. Если мы еще вспомним, что большая часть массы Вселенной заключена в звездах, то напрашивается вывод, что вещество Вселенной, как правило, горячее и плотное. Следует, однако, к этому добавить, что речь идет о современной Вселенной: в далеком прошлом и будущем состояние вещества Вселенной было и будет совсем другим. Об этом речь шла во введении к этой книге.

При температуре порядка десяти миллионов кельвинов и достаточно высокой плотности вещества недра звезды должны быть «наполнены» огромным количеством излучения. Кванты этого излучения непрерывно взаимодействуют с веществом, поглощаясь и переизлучаясь им. В результате таких процессов поле излучения приобретает равновесный характер (строго говоря, почти равновесный характер — см. ниже), т. е. оно описывается известной формулой Планка с параметром T , равным температуре среды. Например, плотность излучения на частоте 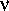в единичном интервале частот равна

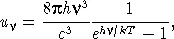(7.1)

в то время как полная плотность излучения задается известным законом Стефана — Больцмана

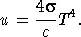(7.2)

Важной характеристикой поля излучения является его интенсивность , обычно обозначаемая символом I . Последняя определяется как количество энергии, протекающее через площадку в один квадратный сантиметр в единичном интервале частот за одну секунду внутри телесного угла в один стерадиан в некотором заданном направлении, причем площадка перпендикулярна к этому направлению. Если для всех направлений величина интенсивности одинакова, то она связана с плотностью излучения простым соотношением