Роджер Пенроуз - Большое, малое и человеческий разум

Рис. 2.10.

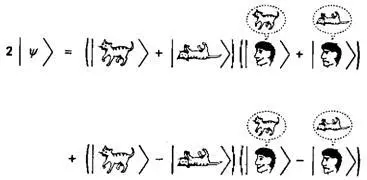
Давайте вернемся к проблеме квантовых измерений и, в частности, к вопросу о квантовой запутанности . На рис. 2.11 приведена запись ЭПР-эксперимента в версии Бома, относящаяся, как уже отмечалось, к Z -тайнам квантовой механики. Проблема сводится к возможностям описания состояния двух частиц со спином ½, которые разлетаются в разные стороны. Полный спин системы равен нулю, поэтому, если мы вдруг узнаем, что спин одной из частиц направлен вверх, то из этого следует, что спин второй частицы направлен вниз. В этом случае квантовое состояние полной системы описывается произведением членов «вверх-здесь» и «вниз-там». Аналогично, состоянию «вниз-здесь» соответствует «вверх-там» (подразумевается, что для проекции спина частицы в состоянии «здесь» мы можем выбрать направления вверх/вниз). Для описания квантового состояния полной системы мы должны внести в рисунок знаки плюс-минус для этих положений (буквы Ни Тна рисунке означают «здесь» и «там», соответственно). В сущности, например, нам следовало бы использовать знак минус для того, чтобы полный спин пары частиц равнялся нулю при любом выборе направления проекции.

Рис. 2.11.

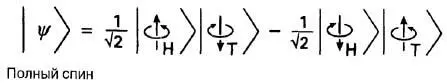
Предположим, что мы измеряем спиновое состояние частицы, попавшей в наш детектор «здесь», а вторая частица за это время улетела очень далеко, и точка «там» находится где-то на Луне! Пусть далее мой коллега на Луне включил детектор и измерил проекцию спина в направлении вверх/вниз. Если спин этой частицы направлен вниз, то это означает, что у первой частицы он был направлен вверх, поскольку обычно предполагается, что вектор состояний частицы представляет собой смесь равновероятных состояний (спин-вверх и спин-вниз).

Для описания систем с такими смешанными состояниями в квантовой механике применяется стандартный метод, основанный на использовании так называемой матрицы плотности . В нашем случае матрица плотности, которую должен ввести первый наблюдатель (его можно условно назвать «я/здесь»), имеет вид, показанный на рис. 2.12. Множители ½ в правой части относятся к вероятности обнаружить, что спин «здесь» направлен соответственно вверх и вниз. При этом речь идет о совершенно обычных, классических вероятностях, отражающих степень нашего незнания относительно реального состояния изучаемой частицы. Эти вероятности представляют собой, как обычно, просто действительные числа (лежащие в интервале между 0 и 1), так что комбинация на рис. 2.12 представляет собой стандартную сумму вероятностей с заданным весом, а не сложную квантовую суперпозицию с комплексными коэффициентами. Отметим еще, что величины типа | < и < | (с угловыми скобками, направленными вправо и влево), которые умножаются на соответствующие вероятности (равные ½), были введены Дираком и названы им кет -вектором и бра -вектором, соответственно. В общем случае бра-вектор представляет собой комплексно сопряженный кет-вектор.

Рис. 2.12.

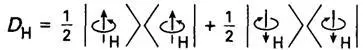
Я не буду рассказывать даже в самых общих чертах о серьезнейшем математическом аппарате теории матриц плотности. Для нашего рассмотрения достаточно знать, что матрица плотности содержит всю информацию, необходимую для расчета вероятностей результатов измерений, производимых над одной частью квантовой системы, в тех случаях, когда информация о другой части квантового состояния недоступна. Например, в нашем случае полное квантовое состояние относится к паре частиц (запутанное состояние), причем предполагается, что при измерении «здесь» мы не можем ничего знать о результатах измерения «там» (на Луне) состояния частицы-партнера.

Я позволю себе немного изменить рассматриваемую ситуацию и предположу дополнительно, что мой коллега на Луне при измерении спина выбрал направление влево/вправо, а не вверх/вниз, как раньше. В этом случае запись состояний примет вид, показанный на рис. 2.13. В сущности, эта запись совпадает с записью рис. 2.11 (та же алгебраическая схема, основанная на геометрии рис. 2.4), однако в ней использованы другие обозначения состояний. В момент измерения мы еще не знаем результатов, полученных коллегой на Луне, однако ясно, что он с одинаковой вероятностью может получить для спина левое направление (в этом случае я должен получить правое направление) или правое (в этом случае я получаю левое). Матрица плотности D H , приведенная на рис. 2.13, при этом будет полностью совпадать с введенной ранее матрицей рис. 2.12. Предлагаемые рассуждения пока кажутся безупречными, поскольку представляется очевидным, что измерения, проводимые коллегой на Луне, не должны изменять вероятностей, получаемых при измерениях на Земле (в противном случае коллега мог бы передавать мне сообщения со скоростью больше скорости света; для этого он мог бы кодировать свои сообщения просто выбором направления регистрации).

Рис. 2.13.

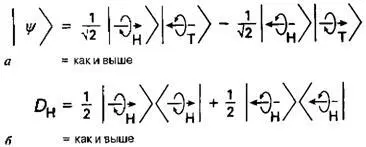
Алгебраически легко проверить, что матрицы плотности действительно одинаковы. Не беда, если вы не знаете, о каких алгебраических приемах я говорю. Вам следует лишь помнить, что матрица плотности — наиболее совершенный аппарат для описания состояния, о части которого вы ничего не знаете. Используемые в этой матрице вероятности имеют обычный смысл, но применяются для квантовомеханического описания, при котором в неявной форме учитываются квантовые вероятности. Короче говоря, если вы ничего не знаете о происходящем «там», матрица плотности даст наилучшее описание состояния «здесь».

Однако из сказанного очень трудно заключить, что матрица плотности описывает реальность . Дело в том, что я позднее могу (или не могу) получить с Луны послание, где будет сказано о том, что мой коллега осуществил измерения состояния второй частицы и получил такие-то и такие-то результаты. Лишь после этого я буду знать о реальном состоянии моей частицы. Матрица плотности не содержит всей информации о моей частице, и я должен определять актуальное состояние связанной пары частиц. Следовательно, матрицу плотности следует рассматривать лишь в качестве средства вспомогательного, временного описания, вследствие чего ее и обозначают иногда сокращением FАРР («для всех практических целей»).