Глеб Анфилов - Бегство от удивлений

После пересказанной притчи Фейнман просит отвлечься от кубиков. Это не вещество, не предметы, не тела. Кубиков не существует. Существует же некая физическая характеристика материи и движения, сохраняющаяся при любых явлениях внутри системы, изолированной от окружающей среды. И далее излагается теорема (из области теории теплоты), которая утверждает, что в надежно изолированном процессе неуничтожимым кубикам соответствует вполне определенная физическая величина, остающаяся постоянной при любых пертурбациях. Это и есть энергия.

К понятию энергии физика шла долго и трудно. Правда, о том, что движение не может пропасть бесследно или родиться из ничего, догадывались давно. Понимали это и Галилей, и еще более четко французский мыслитель Декарт, а за ним наш славный Ломоносов. Но то были слишком общие, чисто качественные, лишенные количественных оценок предположения.

Точность, математический символ, формула родились лишь в XIX столетии. Однако в узких рамках механики сохранение энергии (без употребления этого слова) было известно и Ньютону. Причем в соответствии с сугубо механическими истолкованиями силы (как причины ускорения тел), пути (обязательно в инерциальной системе отсчета), работы (произведения силы на путь). И отправным пунктом послужили-таки мысли о механической работоспособности. Как видите, здесь употреблен тот самый термин, который, как я уже говорил, в обычном, обывательском понимании далеко не всегда отвечает физической сущности энергии.

Сперва несколько простеньких выкладок.

Чтобы повесить у себя над столом портрет Ньютона, я забиваю гвоздь. Бью молотком по шляпке. Гвоздь лезет в стену.

На расстоянии, равном глубине (S) внедрения гвоздя, молоток прикладывает неизменную (это допускается ради простоты) силу F. Тогда при каждом ударе молоток, преодолевая сопротивление стены гвоздю, совершает работу, которая записывается так:

А = F·S.

Между тем, если верить второму закону Ньютона, сила измеряется произведением массы молотка на изменение его скорости во время удара. Это тоже легко записать математически. Пусть молоток, вгоняя гвоздь, затормозился от скорости v до полной остановки за время t. Тогда изменение его скорости (здесь не ускорение, а замедление, которое ради упрощения будем считать равномерным) составило: а = v/t , а сила F = mv/t

Поэтому на расстоянии S = at 2/2 = vt/2 была совершена работа

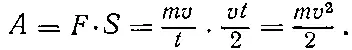
Эта работа выполнена за счет энергии движущегося молотка, которая, таким образом, равна этой же величине T= mv 2/ 2 — и называется кинетической энергией.

Только что добытая формула, выведенная Ньютоном, — целый рог изобилия научных откровений. По ней очень легко предсказывать, какую работу совершит движущееся тело, если его остановить. Пуля убивает волка, вода льется на лопасти турбины, брошенный камень сшибает с ветки яблоко — всюду затрачивается работа. И количество ее дается величиной Т. В этом смысле кинетическая энергия — действительно показатель механической работоспособности тела, «обещание» работы.

Напоминая вам эти школьные истины, скажу еще несколько слов о другом виде энергии — потенциальной.

Я живу в пятиэтажном доме на пятом этаже и горжусь этим. Потому что жильцы, обитающие на нижних этажах, по одному существенному признаку мне заметно уступают. Я гораздо богаче их именно потенциальной энергией.

Чем выше тело над земной поверхностью, тем больше затрачено работы на его подъем. Тяжелый чемодан поднять на пятый этаж труднее, чем легкий. А на третий этаж его поднять легче, чем на пятый. Значит, работа подъема П тут зависит от веса (обозначим его теперь через р) и от высоты подъема h:

П = ph.

А так как вес р равен массе m, помноженной на ускорение свободного падения g, то можно написать формулу:

П = mgh.

Такой величиной измеряется потенциальная энергия, иначе говоря, возможность движения, запасенная в поднятом теле: ведь истраченная работа не пропадает, а остается при чемодане в виде возможности упасть, скатиться, спуститься на веревке. В поднятом теле есть неиспользованная способность к движению, к скорости — значит, и к кинетической энергии. Так же, как в расслабленной руке есть неиспользованная способность совершить удар молотком. Слово «потенциал» в переводе с латыни означает «возможность». Это, как видите, не работа.

Это — запас работоспособности. Потенциальная энергия переходит в кинетическую, а та — в работу. И наоборот. Во всех движениях, где так или иначе совершается работа, происходят эти переливы.

Особенно легко их заметить во всевозможных аттракционах. Качели, гигантские шаги, спиральные спуски, лыжные трамплины — неплохие наглядные пособия для начинающих знатоков механики.

Когда речь заходит об энергии, популяризаторы да и ученые (вплоть до самого Эйнштейна) любят вспоминать аттракцион, который называется русскими горками.

Тележка с седоками скатывается по рельсам с крутого склона, взлетает с разгона на другой, опять скатывается, поднимается на третий и т. д. Сперва потенциальная энергия переходит в кинетическую, потом наоборот: кинетическая в потенциальную и т. д. Причем вот существенная подробность: каждая последующая горка сделана немного ниже предыдущей. Почему?

Потому что полная энергия тележки, то есть сумма ее потенциальной и кинетической энергий, в пути не может увеличиться. Это строго вытекает из законов падения тел (ведь тележка именно падает, хоть и несвободно: по извилистому пути скатывается с вершины горки вниз). В падении с нулевой начальной скоростью нельзя подняться выше точки старта. На это не хватит энергии.

Конечно, при отсутствии трения и сопротивления воздуха полная энергия Е не уменьшилась бы, а сохранилась. Было бы всегда

Е = Т + П = const.

Вот они, механические «кубики Монтигомо»! Сохранение энергии в механической системе тел. Как видите, именно полная энергия остается постоянной. Для тела, двигающегося в поле тяжести, формула записывается так:

Е = mv 2/2 + mgh = const.

Не будь на свете трения и сопротивления воздуха, вершины русской горки можно было бы все расположить на одной высоте и взлетать на них сколько угодно раз. Соедините такие идеальные вершины в кольцо — и на них можно было бы пуститься в вечный безостановочный галоп.

Но в реальных условиях часть кинетической энергии в пути безвозвратно теряется — расходуется на работу против сил трения. Поэтому вершины горки приходится устраивать «мал мала меньше» и в конце концов с огорчением вылезать из остановившейся тележки.