Глеб Анфилов - Бегство от удивлений

Да, именно часы — ведь никакое измерение нельзя даже мысленно исполнить мгновенно, это мы с вами хорошо уяснили в десятой главе, когда рассуждали о предельности скорости света и других особенностях эйнштейновского толкования природы.

Таким образом, определение расстояний, как и всякий измерительный процесс, — совершенно очевидное физическое исследование. Тут геометрия зримо оборачивается физикой, физикой пространственных движений.

Пока, впрочем, забудем о часах. Допустим, что мы умеем измерять длины мгновенно. Это разрешено в физике медленных по сравнению со светом движений, в физике Ньютона. И поставим первую простенькую задачку.

Пусть даны две точки А и В — концы разведенных и крепко свинченных ножниц. И пусть расстояние между ними нужно определить по поверхности. Сразу задаем вопрос: по какой поверхности?

Ну, сперва по шаровой.

Хорошо. Подставим под ножницы глобус. Кратчайшее расстояние на его сфере физик проведет вдоль нити, натянутой между A и В по шаровой поверхности. Оно отмеряется, очевидно, не прямой линией, а кривой — дугой большого круга.

Далее. Посадим наши точки на какую-нибудь седловидную поверхность. Расстояние, проложенное туго натянутой ниткой, будет пройдено по другой кривой линии — гиперболе.

Если же концы ножниц приложить к поверхности письменного стола, то расстояние между ними отмерится по линии, которую мы привыкли называть прямой.

Вот, кажется, добрались до прямизны. Срезав ножом седло или шар, получаем поверхности, в которых линии кратчайших расстояний — наикратчайшие. Так как будто?

Но можно ли быть абсолютно уверенным, что линия на столе абсолютно прямая? И что сам стол плоский?

Кажется, вопросы надуманные. Кажется, плоскость потому и плоскость, что она прямее всех поверхностей.

В действительности дело обстоит сложнее. Все зависит от пространства, в котором стоит наш стол. Само пространство, с точки зрения геометра, вправе быть искривленным. И в конечном счете именно от кривизны пространства зависят кратчайшие расстояния.

Для новичка это очень странные слова — «кривизна пространства». Чтобы привыкнуть к ним, ответим сначала на несколько риторических вопросов.

Как мы узнали, что глобус круглый?

Посмотрели на него со стороны, из окружающего пространства.

Как мы узнали, что классная доска прямая?

Взглянули на нее откуда-то сбоку, опять-таки из окружающего пространства.

А как узнать, прямое ли само пространство?

И на пространство «поглядеть сбоку»? Но это невозможно. Нельзя покинуть пространство, выйти из него, как из дома, чтобы полюбоваться на него издали. Как ни убегай из него, все равно останешься в нем же.

Выходит, нет способов определить, кривое пространство или прямое?

Попробуем все же поискать их. Попробуем исследовать пространство изнутри, не выходя из него. Но не сразу.

Я сперва расскажу, как решается аналогичная задача для поверхности: постараюсь узнать, какова поверхность, не глядя на нее «сбоку», а находясь непосредственно на ней.

Ради наглядности я готов «разбиться в лепешку». Буквально так.

Смотрите: я полностью теряю свой рост, объем, превращаюсь в бесконечно тонкий блин и оказываюсь либо на сфере, либо на седле, либо на плоскости — сам не знаю где.

В качестве этого поверхностного новосела я получаю от вас задание: не сходя с поверхности, определить, какова она.

Условия задания. Сперва — затрудняющие.

Допускается, что я — маленький блин, а поверхность большая, причем в сколь угодно малых участках она сколь угодно мало отличается от плоскости. Кроме того, я близорук, а потому могу обследовать, не сдвигаясь с места, только ближайшие участки поверхности. И вижу лишь то, что находится на ней.

А вот условия, облегчающие решение.

Ползать по поверхности мне разрешено, и сколь угодно далеко. Наконец, считается, что я разумный блин. Умею рассуждать и чертить геометрические фигуры.

Что же мне, блину, делать?

А вот что.

Я намечаю на поверхности две точки — А и В. Соединяю их туго натянутой, но не отделяющейся от поверхности ниткой. По этой нитке провожу линию. И называю ее прямой.

Основания для такого названия у меня есть: во- первых, линия идет по кратчайшему расстоянию между А и В, а во-вторых, из-за сугубой близорукости я вижу вокруг себя плоские участки поверхности. Это, естественно, наводит меня на предположение, что и вся она плоская.

Затем я ставлю на поверхности произвольную точку С, не лежащую на прямой АВ, и пытаюсь провести через нее прямые линии, которые нигде не пересекутся с моей первоначальной прямой.

Я усердно работаю. Ползаю туда-сюда, тяну нитки, провожу линии. В конце концов построение закончено. И я прихожу к одному из трех выводов:

Через точку С проходит только одна прямая линия, не пересекающаяся с АВ.

Удается построить сколько угодно таких линий (прямейших, но не прямых).

Нет ни одной прямейшей линии, которая, проходя через С, не пересекалась бы с АВ.

В первом случае моя поверхность — наверняка плоскость. Во втором — седло или какой-нибудь граммофонный раструб. В третьем — сфера либо что-нибудь вроде яичной скорлупы.

Вот смотрите сами:

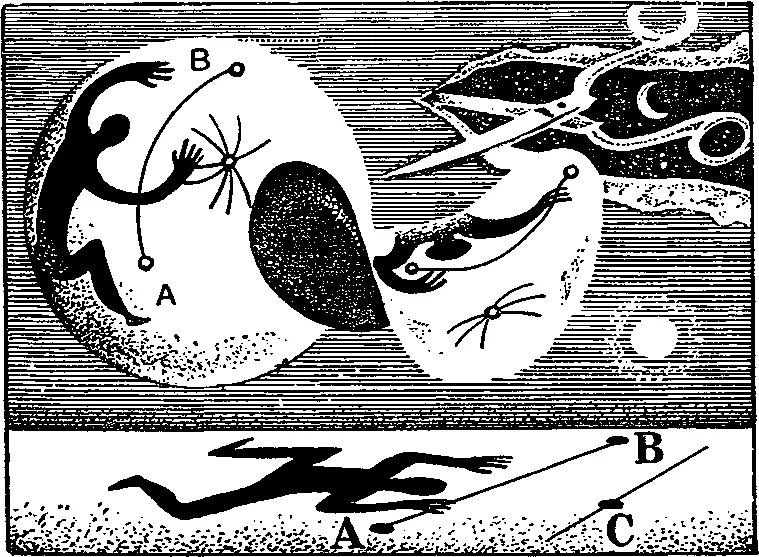
При взгляде «со стороны» лишь для плоскости оправдалось как будто название «прямая» в применении к кратчайшей линии. На непрямых же поверхностях кратчайшие расстояния отмерились по кривым. Вслед за геометрами я называю их геодезическими (сюда относятся, например, экватор и меридианы глобуса, а параллели не относятся: не по ним отмериваются на земном шаре кратчайшие расстояния).

Я все еще блин. Побывал на сфере и седле, теперь переведен на плоскость. Хлопочу о возврате высоты и объема, но пока безуспешно. И от нечего делать занимаюсь геометрией. Это тем более любопытно, что мне на плоскость прислали два отличных инструмента — транспортир и мерную рулетку. Могу измерять длины и углы (по-прежнему — мгновенно, то есть в рамках классической физики).

Отправной пункт моих рассуждений — тот самый постулат о единственности прямой, не пересекающейся с данной прямой, по которому без всяких доказательств устанавливается, что поверхность — плоскость. В давние времена великий греческий геометр Евклид вывел из этого постулата всю геометрию плоскости — планиметрию.

Следом за Евклидом я строю углы, треугольники, квадраты, делаю всевозможные отсчеты, доказываю теоремы. Постепенно я убеждаюсь, что на плоскости действует строгая система правил измерения расстояний. Геометры называют эти правила метрикой.