Глеб Анфилов - Бегство от удивлений

На том же условии нетрудно доказать и другую теорему — о том, что не только в плоских, но и пространственных треугольниках сумма углов составляет два прямых. Раз уж, согласно Евклиду, через любые три точки пространства можно провести плоскость, то и любой пространственный треугольник обязан быть плоским. Но так ли обстоит дело в действительности? Будут ли впору «прямые» штаны и «прямая» шляпа реальному пространству?

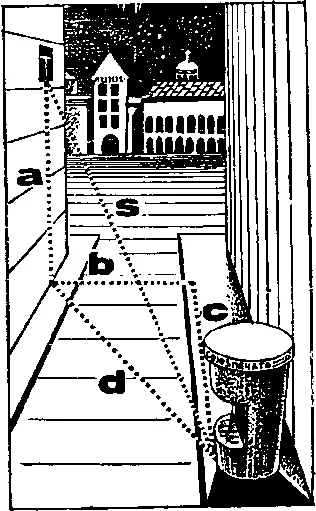Что ж, из всего этого следует как будто немудрящий рецепт облачения пустоты в «пифагоровы штаны» и «треугольную шляпу». Надо проделать измерения длин и углов в реальных пространственных треугольниках. И таким способом «испытать пространство на кривизну».

Ночью, чтобы не мешать уличному движению, я протягиваю веревку из своего окна к далекому киоску. Тщательно измеряю расстояние S. Столь же точно измеряю длины а, b и с. Возвожу их в квадрат, складываю, сравниваю. Вышло подтверждение формулы

S 2= а 2+ b 2+ с 2— значит, в пространстве можно провести плоскости и прямые, значит, пространство плоское, евклидово.

Или так. Еду на Кавказ. Стягиваю тугими канатами три горные вершины. Измеряю в этом треугольнике углы, складываю их. Получилось в сумме два прямых — есть еще одно доказательство того, что пространство плоское.

Ну, а если эти эксперименты приведут к другим результатам? Если S 2не совпадет с а 2+ b 2+ с 2? И сумма углов кавказского треугольника не даст двух прямых? Очень нелегко, очень непривычно допустить подобное. Разум упрямо противится даже мысленно позволить столь странный итог пространственных измерений.

Однако вопреки протестам интуиции заставим себя вообразить, что расхождения все-таки обнаружились. Что это может значить?

Когда подобное случалось на поверхности, вывод был очевиден: поверхность имеет кривизну. А когда нарушения традиционной теоремы Пифагора объявятся в пустоте, резонно будет сказать, что это доказывает кривизну пространства. Прежде, будучи блином, я с помощью метрических теорем определял, какова моя поверхность, не сходя с нее. Теперь, став объемным геометром, я хочу совершенно аналогичным способом узнать, каково пространство: насколько и как оно искривлено. И снова—не выходя из него!

На сфере или седле я не мог построить плоскость и провести идеальную прямую линию. Вместо нее у меня выходили геодезические линии — прямейшие, но не прямые. Именно по ним шли кратчайшие расстояния между точками. Подобно этому, в кривом пространстве я не могу построить ни идеальной прямой, ни идеальной плоскости. Вместо плоскостей проведутся поверхности минимальной кривизны, а вместо прямых опять появятся геодезические линии — прямейшие, но не прямые. Однако изнутри, из пространства, непосредственно увидеть искривление его невозможно, потому что тамошние жители сделают кривыми все свои линейки и другие эталоны прямизны — подгонят их к располагающимся по геодезическим линиям световым лучам, натянутым нитям, путям инерционного полета тел, не подверженных действию сил, и т. д. Поверхности минимальной кривизны будут выглядеть плоскостями. Только исследования параллельных линий да метрические эксперименты помогут определить эту странную, почти невообразимую кривизну пустоты.

Трудновато? Да, нелегко.

Геометрическая возможность неевклидового пространства была неожиданным откровением науки XIX века.

Это открытие, сделанное в 1825 году, принадлежит гениальному русскому математику Николаю Ивановичу Лобачевскому.

Итак, мы с вами добрались до кривого пространства. Научились, кажется, устанавливать изнутри его сам факт кривизны: об этом может свидетельствовать нарушение евклидовых метрических теорем.

Геометры идут дальше: они умеют предсказывать, как именно изменится теорема Пифагора и сумма углов треугольника в пространствах, искривленных по-разному. Рассуждения похожи на те, что я вел, будучи блином на неизвестной поверхности. Например, если а 2+ b 2+ с 2меньше, чем S 2, а сумма углов треугольника меньше двух прямых («пифагоровы штаны» и «треугольная шляпа» для пустоты «малы»), то пространство гиперболическое. Вместо плоскостей в нем седловидные поверхности, вместо прямых — гиперболы. Этот вариант неевклидовой геометрии и был разработан Лобачевским.

Другая геометрическая система, развитая замечательным немецким математиком Георгом Риманом, получится, если а 2+ b 2+ с 2выйдет больше, чем S 2, а сумма углов треугольника превысит два прямых. Эта геометрия называется эллиптической. В ней вместо плоскостей — поверхности вроде яичной скорлупы или мяча, вместо прямых — дуги больших эллипсов или, соответственно, больших кругов.

Позволю себе повторить еще раз: в плавно искривленном пространстве все геодезические линии представляются прямыми. «Истинных» же прямых там нет, их невозможно провести. Любая неизбежно согнется, как обязательно согнется нить, натянутая по сфере. Причем, если пространство искривлено неравномерно, в разных местах по-разному, то и прямейшие геодезические линии в разных точках согнутся неодинаково. При движении вдоль геодезической ее «волнистость», конечно, незаметна. Всюду эта линия выглядит одинаково прямехонькой. Однако стоит испытать в разных местах метрические правила, как обнаружатся изменения, отклонения от привычной евклидовой «нормы».

Короче говоря, в неравномерно-неевклидовом пространстве от точки к точке меняется метрика, приемы определения расстояний. Меняется теорема Пифагора. В общем виде простая формула ее заменяется более сложной, включающей величины, которые характеризуют кривизну пространства в разных его местах. И, как следствие, в разных местах такого пространства оказываются разными длины предметов, кратчайшие расстояния между точками.

Вот такие чудеса допускают геометры в неевклидовом пространстве!

Еще диковина: некоторые неевклидовы пространства могут быть конечными, хоть и безграничными. Расстояния там не превышают некоего определенного значения и, соответственно, не могут существовать сколь угодно большие объемы.

Подобно тому, как яйцо или мяч обладают безграничной поверхностью, но ограниченной площадью, эллиптическое пространство не имеет границ и тем не менее имеет конечный объем. Искривляясь оно как бы замыкается на себя!

Странно? Очень.

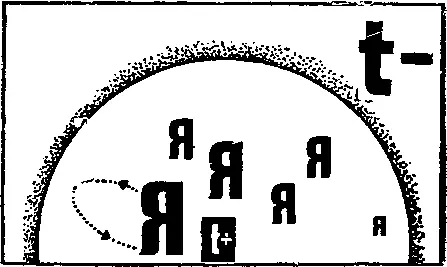
Но все же доступно наглядному моделированию.