Владимир Секерин - Теория относительности — мистификация ХХ века

Вывод, подобный изложенному, можно получить в более общем виде, обращаясь непосредственно к уравнениям Максвелла, нековариантность которых к преобразованиям Галилея считается несомненной. Покажем, что это не так, что нековариантность заложена не в самих уравнениях, а в тех произвольных искажениях, которым они были подвергнуты уже после смерти их автора некоторыми учеными.

Напишем первую группу уравнений Максвелла в том виде, как он писал ее сам в своем «Трактате» [9], заменив лишь его обозначения современной символикой.

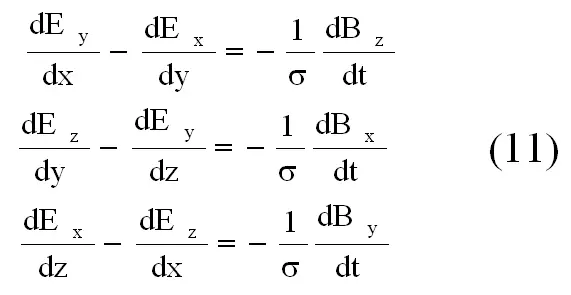
Здесь обозначено: B — магнитная индукция, E — напряженность электрического поля; обе величины являются функциями от четырех аргументов x, y, z и t .

Такими же буквами с индексами x, y, z обозначены проекции этих величин на координатные оси.

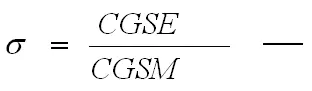
электродинамическая постоянная, численно равная скорости света в пустоте относительно его источника, но физически ей не тождественная.

Заменяя в системе (11) проекции B и E их выражениями через соответствующие орты B x = iB, B y = jB, B z = kB , получим после векторного сложения в левой части ротор напряженности электрического поля, а в правой части — полную производную магнитной индукции. Следовательно, система уравнений (11) преобразуется в одно:

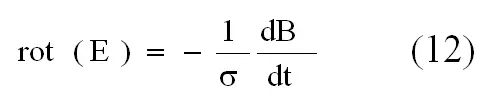
Точно такое же уравнение Максвелла в дифференциальной форме выводит Э. Парселл во II томе «Берклеевского курса физики» [10], исходя из его интегральной формы

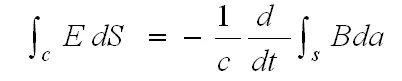
Он показывает, что уравнение (12) является следствием этого последнего уравнения. Но логика следующего далее утверждения того же Э. Парселла совершенно парадоксальна, он пишет буквально следующее:

«Так как B может зависеть от положения и от времени, то мы напишем δB/δt вместо dB/dt». Никаких иных пояснений или доказательств к этому неожиданному заявлению не дается. Да их и не может быть! Зная зависимость B (как и E ) от четырех аргументов x, y, z и t , о чем беспристрастно Э. Парселл пишет на странице 245 своей книги [10], он предлагает исключить из рассмотрения три из них и оставить только один и именно тот, который в предыдущем математическом анализе явно не фигурировал, а совершенно произвольно внесен в последний момент!

В других курсах релятивистской физики такой прием лучше замаскирован. Приведем лишь некоторые наиболее известные и распространенные источники.

Р. Фейнман в своих «Фейнмановских лекциях по физике» рассматривает формулы электромагнитного поля с частными производными по времени, называя их не уравнениями Максвелла-Герца, как Эйнштейн, а уравнениями Максвелла, хотя, как было показано выше, Максвелл, следуя Фарадею, использовал в них полные производные. Р. Фейнман пишет [11]: «Однако уравнения Максвелла, по-видимому, не подчиняются принципу относительности: если их преобразовать подстановкой (Галилея — С. Б., М. В .), то их вид не останется прежним». Но Р. Фейнман мог бы сделать совершенно другой вывод, если бы он рассматривал уравнения электромагнитного поля именно в форме Максвелла!

В курсе физики С. Э. Фриша и А. В. Тиморевой [12], в справочнике по физике для студентов Н. И. Карякина… [13] и многих других монографиях уравнения Максвелла приводятся в частных производных по времени без всяких обоснований.

На странице 46 своего курса физики С. Э. Фриш и А. Д. Тиморева [12] дают краткий вывод уравнения Фарадея

из которого позднее получаются уравнения Максвелла. Однако при выводе этого равенства авторы забыли, что в общем виде как напряженность E , так и потенциал u зависят не только от абсциссы рассматриваемой точки, но и непосредственно от времени t , в течение которого может меняться возбуждение излучающего центра всей системы E = E(n, t). По этой причине равенство (*) нуждается в исправлении:

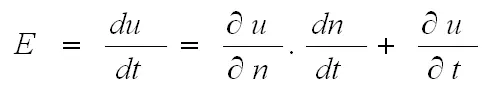
Такие же двучленные выражения должны быть написаны и для каждого из прочих координатных направлений. Только после этого их система будет оправдана всеми экспериментами Фарадея и на их основе можно будет построить современную, а не воображаемую, электродинамику. При этом именно члены типа δu / δt обеспечат ей возможность охвата как статических, так и быстротекущих явлений.

Но авторы этого учебника членами δu / dt пренебрегают, что лишает их выводы необходимой общности. Позднее, на стр. 462–466, с вводом новой переменной D возвращается связь электромагнитного поля со временем, но одновременно теряется связь правых частей уравнений Максвелла (и Фарадея) с пространственными координатами. А в них то и заключается самая сущность вопроса.

Понятно, что искаженные таким образом уравнения не могут дать правильных результатов.

Для дальнейшего исследования мы возвратимся к исходному уравнению Максвелла в его общей форме (12).

Развернем величину полной производной по частным ее слагающим

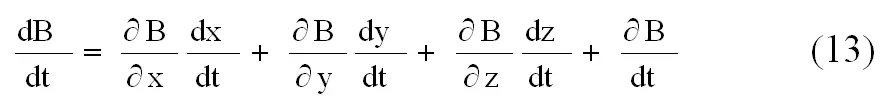
Производные от координат по времени, согласно условиям принятым в предыдущем разделе, равны слагающим скорости движения света. Следовательно, равенство (12) равносильно следующему:

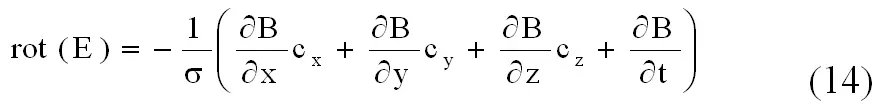
Такое же уравнение мы можем написать для любой другой (штрихованной) системы координат, движущейся относительно первой в любом направлении со скоростью v :

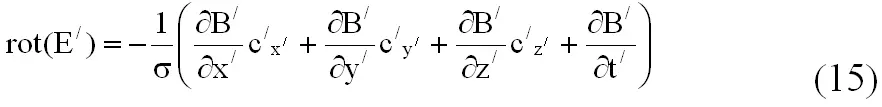
Оба уравнения (14) и (15) относятся к одному и тому же явлению в одном и том же единственном пространстве. Следовательно, они должны быть совместны. Свяжем их в соответствии c правилами аналитической геометрии преобразованиями Галилея по всем координатам:

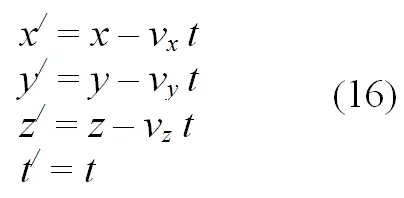
После дифференцирования равенства (16) имеем:

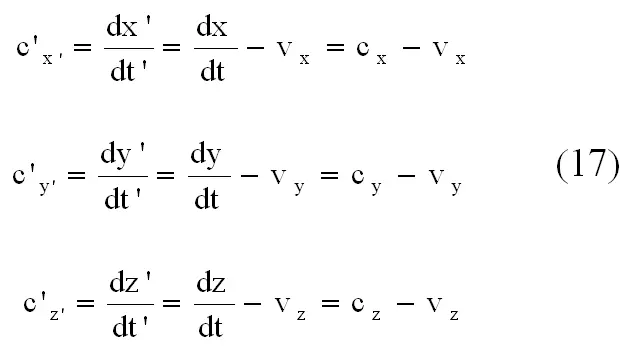
Подставляя эти соотношения в уравнение (15), получим: