Кудрявцев Степанович - Курс истории физики

Максвелл определяет вероятность того, что частица пройдет заданное расстояние до того, как она столкнется с другой частицей, и находит ее равной

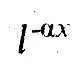
, где х - заданное расстояние. Среднее расстояние, проходимое каждой частицей до столкнлвения, равно l =1/α. Он показывает далее, что давление, вызванное ударами частиц о стенку, выражается формулой:

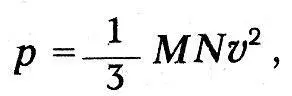
где N - число частиц в единице объема, М - масса каждой частицы, v - ее скорость. В выводе Максвелла фигурирует средняя длина свободного пробега, которая выпадает из конечного результата. Полагая MN = ρ - плотность газа,

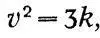
получаем:

p=kρ,

что выражает закон Бойля —Мариотта. При этом константа а выражается через средний квадрат скорости:

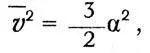
так что

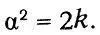
Длину свободного пробега Максвелл определяет из коэффициента внутреннего трения. Рассматривая перенос количества движения («момента», по терминологии Максвелла) между двумя слоями газа, движущимися с различными скоростями, он находит выражение для силы трения, приходящейся на единицу площади:

F = 1/3 MNlv (du/dz) ,

где du/dz — градиент скорости. Полагая F = μ(du/dz), согласно закону трения, находим:

μ =1/3 MNlv = 1/3 ρ lv.

Но длина свободного пробега

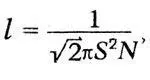
где S - диаметр частицы. Отсюда получаем:

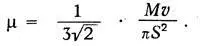
Максвелл пишет, что его уравнение «приводит нас к замечательному выводу», заключающемуся в том, что «коэффициент трения не зависит от плотности. Этот вывод из математической теории является крайне поразительным, и единственный опыт, с которым я встретился в этой области, его как будто не подтверждает». На самом деле, как оказалось, этот вывод подтвердился опытом в широких пределах давлений, но Максвелл считает необходимым «сопоставить свою теорию с тем, что известно о диффузии газов и. о происхождении теплоты через газ». Таким образом, Максвелл исследовал впервые явления переноса. Подводя итоги своим исследованиям, Максвелл писал: «Мы проследили здесь за математической теорией столкновения твердых упругих частиц в различных случаях, в которых, казалось бы, существует аналогия с явлением газов. Мы вывели, как это уже раньше сделали и другие, отношения давления, температуры и плотности для отдельного газа. Мы также доказали, что когда два различных газа свободно действуют друг на друга (а это бывает, когда они находятся при одной и той же температуре), то массы отдельных частиц каждого газа обратно пропорциональны квадрату молекулярной скорости и что, следовательно, при равной температуре и равном объеме количество частиц в единице объема одинаково».

В резюме Максвелла обращает; на себя внимание тот факт, что он ни слова не говорит об открытом им законе распределения скоростей, зато подроб^ но говорит об объяснении закона Аво-гадро. Заметим, что об этом объяснении он всегда упоминал в своих популярных статьях и выступлениях. Между тем мы сейчас видим главную заслугу Максвелла в открытом им законе скоростей и забыли о том, что сам Максвелл считал наиболее важным. Теорию равномерного распределения энергии по степеням свободы мы связываем с Больцманом. Она охватывает открытие Максвеллом равенства средних энергий молекул независимо от их массы при одной и той же температуре и объясняет неудачу его попытки истолковать соотношение теплоемко стей.

В теории Максвелла особенно наглядно видны ее механические предпосылки. Модель твердых упругих шариков, предложенная Максвеллом для объяснения газовых законов, работает по законам механики Ньютона. Максвелл не сомневался в применимости этих законов к атомам и молекулам. Но его поражал один замечательный факт в атомно-молекулярном мире; строгая определенность свойств молекул и атомов. «Молекулы, — пишет Максвелл, — образованы по одному и тому же типу с точностью, какой мы не находим в ощущаемых нами свойствах тел, ими образуемых. Во-первых, масса каждой молекулы и все другие ее свойства абсолютно неизменны. Во-вторых, свойства всех молекул одного рода абсолютно тождественны».

Открытие спектрального анализа вновь подтвердило эту определенность свойств молекул и атомов. «При помощи спектроскопа, — говорил Максвелл, — длины световых волн различного рода можно сравнивать между собой до одной десятитысячной доли. Таким путем убедились, что не только молекулы каких угодно образчиков водорода в наших лабораториях имеют один и тот же ряд периодов колебаний, но что свет с тем же самым рядом периодов колебаний испускается Солнцем и неподвижными звездами. Таким образом мы убеждаемся, что молекулы такой же точно природы, как у нашего водорода, существуют и в отдаленных пространствах... Молекула водорода... находится ли она на Сириусе или на Арктуре, совершает свои колебания в точности в то же самое время. Следовательно, каждая молекула во Вселенной носит на себе печать меры и числа настолько же ясную, как и метр парижских архивов или как двойной царский локоть карнакского храма».

Ум Максвелла останавливается перед этой таинственной, не объяснимой никакими известными в его время естественными причинами загадкой определенности молекул, необычайной устойчивости их свойств. Он сравнивает эту устойчивость с устойчивостью планетных орбит и указывает, что «научное значение этих астрономических и земных величин много ниже фундаментальных величин, образующих молекулярную систему». «Как мы знаем, — пишет Максвелл, — естественные процессы изменяют и в конце концов разрушают весь порядок и размеры как Земли, так и всей солнечной системы. Но если случались и вновь могут случиться катастрофы, если старые системы могут разрушаться и на их развалинах могут возникать новые системы, то молекулы, из которых эти системы построены, неразрушимы и неизменны — это краеугольные камни материальной Вселенной». Максвелл считает, что такая определенность и неизменяемость молекул, придающая им, по выражению Джона Гершеля, «характерные признаки фабричных изделий », «исключает мысль о возможности их вечного существования и самопроизвольного происхождения», т. е. молекулы и атомы должны быть «изготовлены» богом. Так, по Максвеллу, мы подошли к точке, «дальше которой наука идти не может».