Евгений Седов - Одна формула и весь мир

Все полученные Добрушиным искусственные фразы сведены нами в таблицу. К ним добавлена еще одна фраза, которой мы присвоили № 4. Она выписана наугад прямо из текста и, следовательно, соответствует всем грамматическим и фонетическим правилам русского языка Теперь окинем взглядом снизу вверх всю таблицу: перед нами картина распада и деградации: буквы, которые в нижней фразе соблюдали осмысленный строгий порядок, постепенно «сбиваясь с толку», в конце концов настолько между собой перемешались, что превратились в полную абракадабру (фраза № 1).

Превращение фразы № 4 сначала во фразы № 3 и № 2, а затем во фразу № 1 — это модель перехода всякой упорядоченной системы в состояние термодинамического равновесия, то есть такого хаоса, при котором энтропия становится максимальной, а вероятности выравниваются, приближаясь к условию

р 1=р 2= .. =р n= 1/n

Теперь попробуем на те же фразы посмотреть в обратном порядке, перемещая взгляд сверху вниз, от фразы № 1 к фразе № 4. Перед нами предстанет модель всех накапливающих порядок антиэнтропийных процессов Элементы системы (в рассматриваемом случае система — это текст, а элементы системы — отдельные буквы) сначала следуют друг за другом в любых сочетаниях, не соблюдая правил, не «обращая внимания» на то, какие элементы появились до них (фраза № 1). Первый проблеск порядка появился после того, как частоты появления элементов системы стали соответствовать вероятностям появления тех же элементов в структуре реальных упорядоченных систем (фраза № 2). Порядок в системе существенно увеличился после того, как стали учитываться вероятности сочетаний ее элементов, определяемые правилами образования слогов в тексте (фраза № 3).

«Полный порядок» образовался с того момента, как стали учитываться все правила русского языка (фраза № 4).

С каждым шагом от хаоса к упорядоченности все меньше и меньше становится энтропия системы, потому что все больше и больше отличаются друг от друга различные вероятности Pi входящие в формулу энтропии:

Стало быть, окинув взглядом сверху вниз таблицу, мы увидели, как протекает типичный антиэнтропийный процесс.

Подобная «антиэнтропийная метаморфоза» может происходить не только с текстом, но и с системами самой разнообразной природы. Например, можно представить себе, как молекулы жидкости, метавшиеся из стороны в сторону в хаотичном броуновском движении, для которого все скорости и направления в равной степени вероятны, начали вдруг выстраиваться в упорядоченные «колонны» и «шеренги» (потому что вероятности направлений движения стали различными) и постепенно образовали сложный, многогранный кристалл. А можно вообразить, как из сумбура нечленораздельных звуков начали образовываться закономерные сочетания (звуковые сигналы), которые постепенно превратились в осмысленные слова.

Как в этих, так и во многих других процессах, приводящих к увеличению порядка в структуре формирующихся систем, происходит накопление информации, количество которой определяется с помощью той же функции

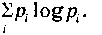
Известный физик Леон Бриллюэн показал, что количество накопленной и сохраняемой в структуре систем информации 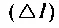в точности равно уменьшению их энтропии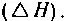

Посмотрим, как это общее правило (так называемый негэнтропийный принцип информации) проявляется на частном примере рассмотренных нами фраз.

С помощью функции подсчитали, что при переходе от фразы № 1 к фразе № 4 энтропия текста уменьшилась примерно в 5 раз. Для фразы № 1 энтропия (неопределенность появления каждой новой буквы) составляет 5 бит. Во фразе № 2 неопределенность появления каждой буквы уменьшается на 1 бит и составляет 4 бита на букву. Энтропия реальных текстов меньше, чем максимальная энтропия (фраза № 1) на 4 бита. Она составляет около 1 бита на букву 7 7 Все значения энтропии и информации в битах подсчитываются с помощью функции Пример I. Энтропия сообщений типа «У А. родилась дочка», «В. играет белыми» равна: 1бит Пример II. Энтропия появления каждой следующей буквы в тексте равна: Пример III. Для фразы: № 1 выполняется условие р А = Рб =... = = Ря= 1/32 Подстановка этих значений р А , р Б , р в ,..., р я в общее выражение примера II дает энтропию 5 бит. Пример IV. Чтобы определить энтропию фразы Я? 2, достаточно подставить в общее выражение примера II реальные значения вероятностей букв в русских текстах (Po = 0,09, P ф = 0,002 и др.). В результате такой подстановки получим значение энтропии около 4 бит. Пример V. Чтобы определить энтропию фраз № 3 и № 4, необходимо учитывать не только вероятности отдельных букв, но и вероятности их сочетаний. Для реальных текстов эта задача становится настолько сложной, что приходится применять приближенные методы расчета, описанные подробно и доступно в книге А. М. Яглома и И. М. Яглома «Вероятность и информация» (глава 4). Приближенное значение энтропии реальных текстов составляет около 1 бита на букву .

*Все значения энтропии и информации в битах подсчитываются с помощью функции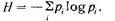

Пример I. Энтропия сообщений типа «У А. родилась дочка», «В. играет белыми» равна: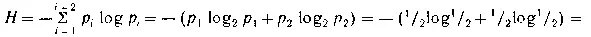

= 1 бит

Пример II. Энтропия появления каждой следующей буквы в тексте равна:

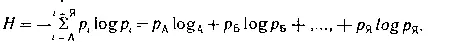
Пример III. Для фразы :№ 1 выполняется условие р А= Рб =... = Ря= 1/32

Подстановка этих значений р А, р Б, р в,..., р я в общее выражение примера II дает энтропию 5 бит.

Пример IV . Чтобы определить энтропию фразы №2, достаточно подставить в общее выражение примера II реальные значения вероят­ностей букв в русских текстах (Po= 0,09, P ф=0,002 и др.). В результате такой подстановки получим значение энтропии около 4 бит.

Пример V . Чтобы определить энтропию фраз № 3 и № 4, необ­ходимо учитывать не только вероятности отдельных букв, но и веро­ятности их сочетаний. Для реальных текстов эта задача становится настолько сложной, что приходится применять приближенные методы расчета, описанные подробно и доступно в книге А. М. Яглома и И. М. Яглома «Вероятность и информация» (глава 4). Приближенное значение энтропии реальных текстов составляет около 1 бита на букву.

Уменьшение энтропии реальных текстов по сравнению с фразой № 1 обусловлено тем, что в структуре реального текста содержится информация всех грамматических и фонетических правил русского языка. Разность между энтропией реального текста Н р = 1 бит на букву и максимальной энтропией фразы № 1, Hmax =5 бит на букву — это и есть количество информации I п , содержащейся в грамматических и фонетических правилах, которым подчиняются реальные тексты. Таким образом: