Яков Гегузин - Живой кристалл
- Название:Живой кристалл
- Автор:
- Жанр:
- Издательство:«Наука»
- Год:1981
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Яков Гегузин - Живой кристалл краткое содержание
Книга содержит научно-популярное изложение современных представлений о физических явлениях и процессах, которые происходят в реальных кристаллах и определяют их физические свойства и эксплуатационные характеристики. Рассказано о движении атомов, составляющих решетку, о характеристиках и свойствах различных дефектов строения реальных кристаллов, о том, как кристалл хранит воспоминания о своем прошлом, повлиявшем на его структуру. Используемые в книге формулы вполне доступны овладевшему лишь начальными сведениями из алгебры.
Книга рассчитана на всех лиц, интересующихся современным естествознанием.
Живой кристалл - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Серьезный успех: мы придумали элементарную модель теплового движения в кристалле и получили закон Дюлонга и Пти. Прочтем наш результат немного по-иному: согласующийся с нашим расчетом и экспериментально подтвержденный закон Дюлонга и Пти свидетельствует о том, что мы, видимо, правильно понимаем характер теплового движения атомов в кристалле, воплощенный в нашей модели.
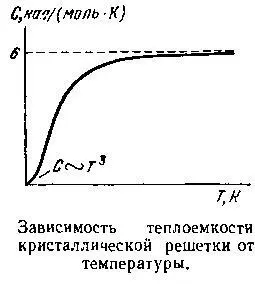
Все сказанное — правда, однако не вся правда. Хочется сказать так: только «высокотемпературная» часть правды. Дело в том, что прошло не более десяти лет после открытия Дюлонга и Пти, как было обнаружено, что некоторые тугоплавкие вещества, например алмаз, не подчиняются этому закону. А потом было установлено, что теплоемкость таких веществ не является постоянной, как это предсказывает закон Дюлонга и Пти, а увеличивается с ростом температуры, стремясь к тому значению, которое законом предусматривается.
Со временем, когда научились экспериментировать в области низких температур, выяснилось, что особенность поведения тугоплавких веществ — никакая не особенность, а, наоборот, является нормой для всех веществ.
Эта «особенность» впервые обнаружилась на тугоплавких веществах просто потому, что «комнатная» температура по сравнению с их температурой плавления низка. Закон Дюлонга и Пти, обнаружившись, выглядел откровением, а на поверку оказался лишь долей правды, ее «высокотемпературной» частью!
Отвлечемся от того чувства разочарования, которое, видимо, испытывал Дюлонг (Пти ушел из жизни вскоре после открытия закона). Закроем пока глаза на «низкотемпературную» правду и тщательнее вдумаемся в открытие французских физиков: «низкотемпературная» правда не отменяет справедливости закона Дюлонга и Пти в области высоких температур, где закон может быть использован для уточнения характеристик теплового движения атомов.
Из закона Дюлонга и Пти, разумеется применительно к той области температур, где он подтверждается экспериментально, следует, что, участвуя в тепловом движении, атомы в узлах решетки колеблются подобно обычным маятникам. До сих пор мы довольствовались лишь знанием энергии этих колебаний. А теперь построим элементарную теорию колебаний атома в кристалле и установим амплитуду А и период τ 0этих колебаний.
Немного упростим модель кристалла. Пусть атомы, окружающие данный «одиночный» атом, колебаний не совершают, а лишь, взаимодействуя с колеблющимся, определяют силы притяжения и отталкивания, которые действуют на него в соответствии с потенциалом взаимодействия между ним и окружающими атомами. И еще больше упростим реальную ситуацию, допустив, что атом совершает колебания лишь вдоль определенной прямой, а не во всех трех направлениях в пространстве. В рамках такой модели естественно атом, колеблющийся в узле решетки, мысленно заменить грузиком, колеблющимся на пружинке: грузик — атом, пружинка — упругое окружение. К помощи пружинки мы недавно уже прибегали.
Не увели ли нас предположения и упрощения далеко в сторону от тех реальных условий, в которых колеблется реальный атом в узле реальной кристаллической решетки? Кажется, не увели. Пружинка удачно моделирует наличие силы притяжения (когда она растянута) и силы отталкивания (когда она сжата). Грузик хорошо моделирует атом, так как в нашей задаче, если силы заданы, от атома требуется лишь иметь определенную массу, а грузик ее имеет. А то, что в избранной модели колебания происходят вдоль прямой, существа дела практически не искажает, так как более сложное колебание можно представить в виде суммы прямолинейных, — этой возможностью мы уже пользовались, когда, объясняя открытие Дюлонга и Пти, предполагали, что каждый из атомов участвует в трех прямолинейных колебаниях.
Определим вначале амплитуду колебаний атома. Потенциальная энергия W п колеблющегося грузика, очевидно, не должна зависеть от того, смещается он влево или вправо от своего среднего положения, когда пружина и не сжата, и не растянута. А это означает, что
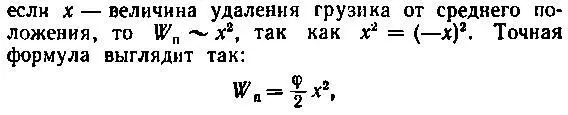
где φ— постоянная величина, характеризующая упругие свойства пружины. Эта величина определяет силу, действующую на грузик со стороны пружины: F = — φх.
При максимальном отклонении колеблющегося атома от положения равновесия, т. е. при отклонении на величину амплитуды колебаний А , как мы уже знаем, вся энергия атома kТ будет запасена в виде потенциальной энергии. Это означает, что
φA 2 / 2 = kT
и, следовательно,
A = (2 kT / φ) 1/2
Полученная формула неприятна тем, что в нее входит неизвестная нам величина φ. Впрочем, ее нетрудно связать с известными характеристиками кристалла. Для этого левую и правую части формулы, которая определяет силу F , поделим на а 2 , где а — межатомное расстояние:
F/а 2 = - φ /а . x / а
Легко усмотреть, что F/a 2 — напряжение, действующее на атом, х/а — относительное смещение атома. Если оно невелико, последняя формула просто является записью закона Гука, а отношение φ/ а имеет смысл модуля упругости Е . Итак, φ = Еа , а амплитуда
A = (2 kT / Ea ) 1/2≈ T 1/2
Из нашего расчета следует, что амплитуда колебаний атома с температурой возрастает по закону T 1/2 . У металлов, для которых Е ≈ 10 12дин/см 2, а ≈ 3• 10 -8см, в области предплавильных температур амплитуда А ≈ 2 . 10 -9см и, следовательно, составляет несколько процентов от величины межатомного расстояния. Много это или мало? Конечно же, немного, если иметь в виду сохранение решетки как таковой, если заботиться о том, чтобы тепловые колебания не расшатали кристалл, лишив его порядка в расположении атомов. При найденной нами амплитуде колебаний атомов кристалл сохраняет свою индивидуальность, еще не теряет «черты кристалла».
Определим теперь период колебаний атома. Если иметь в виду лишь приближенную оценку, то сделать это совсем несложно. Когда вся тепловая энергия колеблющегося атома преобразована в его кинетическую энергию, атом движется с максимальной скоростью, которая следует из условия
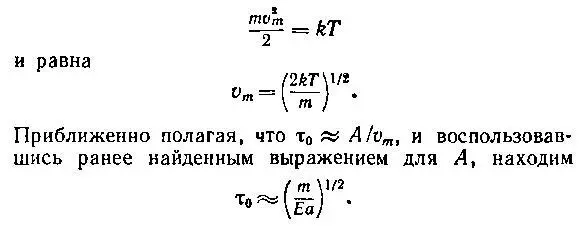
Интервал:
Закладка:







