Александр Китайгородский - Физика для всех. Движение. Теплота

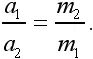
Это значит, что ускорение, которое получит пушка при откате, будет во столько раз меньше ускорения снаряда, во сколько раз пушка весит больше, чем снаряд.

Ускорение пули, а также и ружья при отдаче, длится до тех пор, пока пуля движется в дуле ружья. Обозначим это время буквой t . Через этот промежуток времени ускоренное движение сменится равномерным. Для простоты будем считать ускорение неизменным. Тогда скорость, с которой пуля вылетит из дула ружья, будет v 1= a 1 t , а скорость отдачи v 2= a 2t . Так как время действия ускорения одно и то же, то v 1/ v 2= a 1/ a 2и, следовательно,

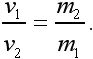
Скорости, с которыми разлетаются тела после взаимодействия, будут обратно пропорциональны массам этих тел.

Если вспомнить векторный характер скорости, то последнее соотношение можно переписать так: m 1 v 1= − m 2 v 2; знак минус говорит о том, что скорости v 1 и v 2 направлены в противоположные стороны.

Наконец, перепишем равенство еще раз – перенесем произведения масс на скорости в одну сторону равенства:

m 1 v 1+ m 2 v 2= 0

Произведение массы тела на его скорость называется импульсом тела (другое название – количество движения). Так как скорость – вектор, то и импульс является векторной величиной. Разумеется, направление импульса совпадает с направлением скорости движения тела.

При помощи нового понятия закон Ньютона F = ma может быть выражен иначе. Так как a = ( v 2− v 1)/ t , то F = ( mv 2− mv 1)/ t , или Ft = mv 2− mv 1. Произведение силы на время ее действия равно изменению импульса тела.

Вернемся к явлению отдачи.

Наш результат рассмотрения отдачи орудия можно теперь сформулировать короче: сумма импульсов орудия и снаряда после выстрела остается равной нулю. Очевидно, такой же она была и до выстрела, когда орудие и снаряд находились в состоянии покоя.

Скорости, входящие в уравнение m 1 v 1+ m 2 v 2= 0, – это скорости непосредственно после выстрела. При дальнейшем движении снаряда и орудия на них начнут действовать силы тяжести, сопротивление воздуха, а на пушку дополнительно – и сила трения о землю. Вот если бы выстрел был произведен в безвоздушном пространстве из орудия, висящего в пустоте, тогда движение со скоростями v 1и v 2продолжалось бы сколь угодно долго. Орудие двигалось бы в одну сторону, а снаряд – в противоположную.

В артиллерийской практике в настоящее время широко применяются орудия, установленные на платформе и стреляющие на ходу. Как же изменить выведенное уравнение, чтобы оно было применимо к выстрелу из такого орудия? Мы можем записать:

m 1 u 1+ m 2 u 2= 0,

где u 1и u 2– скорости снаряда и орудия по отношению к движущейся платформе. Если скорость платформы V , то скорости орудия и снаряда по отношению к покоящемуся наблюдателю будут v 1= u 1+ V и v 2= u 2+ V .

Подставляя значения u 1и u 2в последнее уравнение, получим:

( m 1+ m 2) V = m 1 v 1+ m 2 v 2.

В правой части равенства у нас стоит сумма импульсов снаряда и орудия после выстрела. А в левой? До выстрела орудие и снаряд с общей массой m 1+ m 2движутся вместе со скоростью V . Значит, и в левой части равенства стоит общий импульс снаряда и орудия, но до выстрела.

Мы доказали очень важный закон природы, который называется законом сохранения импульса. Доказали мы его для двух тел, но можно легко показать, что такой же результат имеет место и для любого числа тел. Каково же содержание закона? Закон сохранения импульса говорит, что сумма импульсов нескольких тел, находящихся во взаимодействии, не меняется в результате этого взаимодействия.

Ясно, что закон сохранения импульса будет справедлив лишь тогда, когда на ту группу тел, которую мы рассматриваем, не действуют силы со стороны. Такая группа тел называется в физике замкнутой.

Ружье и пуля во время выстрела ведут себя, как замкнутая группа двух тел, несмотря на то, что испытывают действие силы земного притяжения. Вес пули мал по сравнению с силой пороховых газов и явление отдачи произойдет по одним и тем же законам, независимо от того, где будет произведен выстрел, – на Земле или в ракете, летящей в межпланетном пространстве.

Закон сохранения импульса позволяет легко решать различные задачи, относящиеся к столкновениям тел. Попробуем одним глиняным шариком попасть в другой – они слипнутся и будут продолжать движение вместе; если выстрелить из ружья в деревянный шар, он покатится вместе с застрявшей в нем пулей; стоявшая вагонетка покатится, если человек с разбегу прыгнет в нее. Все приведенные примеры с точки зрения физика весьма похожи. Правило, связывающее скорости тел при столкновениях такого типа, сразу же получается из закона сохранения импульса.

Импульсы тел до встречи были m 1 v 1и m 2 v 2, после столкновения тела объединились, их общая масса равна m 1+ m 2. Обозначив скорость объединившихся тел через V , получим:

m 1 v 1+ m 2 v 2= ( m 1+ m 2) V ,

или

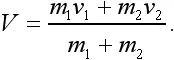
Напомним о векторном характере закона сохранения импульса. Импульсы mv , стоящие в числителе формулы, надо складывать как векторы.

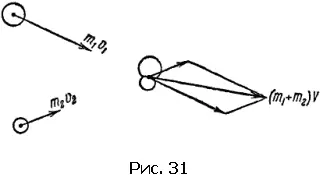
«Объединяющий» удар при встрече движущихся под углом тел показан на рис. 31. Для того чтобы найти величину скорости, надо длину диагонали параллелограмма, построенного на векторах импульсов встречающихся тел, разделить на сумму их масс.

Человек движется, отталкиваясь от земли; лодка плывет потому, что гребцы отталкиваются веслами от воды; теплоход также отталкивается от воды, только не веслами, а винтами. Также отталкиваются от земли и поезд, идущий по рельсам, и автомашина, – вспомните, как трудно автомашине сдвинуться с места в гололедицу.

Итак, отталкивание от опоры – как будто бы необходимое условие движения; даже самолет и тот движется, отталкиваясь винтом от воздуха.

Однако так ли это? Нет ли какого-нибудь хитрого способа двигаться, ни от чего не отталкиваясь? Если вы катаетесь на коньках, то легко можете убедиться на своем опыте, что такое движение вполне возможно. Возьмите в руки тяжелую палку и встаньте на лед. Бросьте палку вперед – что произойдет? Вы покатитесь назад, хотя и не думали отталкиваться ногой от льда.