Борис Шустов - Астероидно-кометная опасность: вчера, сегодня, завтра

Проведем анализ результатов импульсного воздействия на орбиту астероида. Поскольку описываемые действия и соответствующие изменения относительно малы, анализ можно существенно упростить.

Положим, что орбита небесного тела — круговая, с периодом обращения P и радиусом r 0. Обозначим скорость тела через V 0. Далее пусть эта орбита — поражающая, т. е. проходящая в некоторой своей точке либо через центр Земли, либо через зону резонансного возврата. Тогда задачей коррекции орбиты будет являться ее изменение в точке встречи с Землей на величину, позволяющую избежать столкновения (прохождения через зону резонансного возврата). Будем рассматривать импульсное воздействие на астероид, которое представляет собой практически мгновенное изменение его скорости.

Определим гелиоцентрическую инерциальную систему прямоугольных координат XY Z (рис. 10.1). Исходную круговую орбиту астероида разместим в плоскости XY этой системы координат. Результаты изменения орбиты астероида будем характеризовать отклонениями его возмущенных текущих координат по радиус-вектору dr, вдоль орбиты dl и нормали к плоскости орбиты dn от координат в невозмущенном движении. Величины dr, dl, dn удобно рассматривать в астероидоцентрической орбитальной системе прямоугольных координат S, T, W. Ее начало совмещается с текущим положением в невозмущенном движении астероида. Здесь ось S направлена по радиус-вектору орбиты от центра Солнца, ось T направлена по нормали к радиус-вектору и лежит в плоскости орбиты, а ось W дополняет орбитальную систему координат до правой.

Сначала рассмотрим результат приложения малого импульса скорости dV Z, направленного по оси W, т. е. по нормали к плоскости орбиты астероида. Пусть импульс скорости прикладывается в момент нахождения астероида на оси X (рис. 10.1). Анализ показывает, что результатом является изменение наклонения орбиты небесного тела, а все остальные элементы орбиты остаются без изменения. При этом изменение движения астероида относительно первоначальной орбиты сводится к периодическим гармоническим колебаниям лишь по одной координате W. Для малого изменения орбиты колебания dn как функции времени t, отнесенные к радиусу орбиты r 0, могут быть записаны в виде

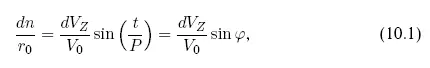
где P — невозмущенный период обращения астероида по орбите, а амплитуда колебаний равна .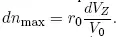

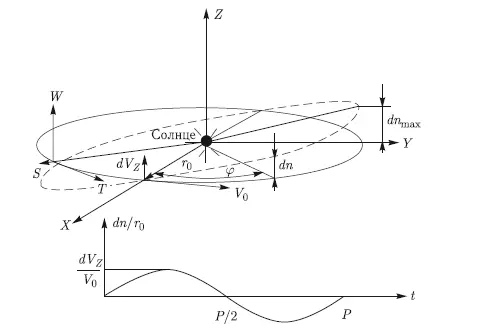
Рис. 10.1. Влияние импульса скорости, приложенного по оси W, на орбиту астероида

Выберем в качестве удобного масштаба текущих отклонений небесного тела в линейных единицах экваториальный радиус Земли R э= 6378 км. Тогда можно получить выражения для величины максимального смещения dn maxпо оси Z и относительного приращения скорости dV Z/V 0, необходимого для обеспечения смещения dn max:

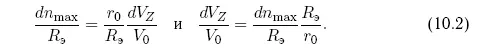
Отметим, что фаза колебания останется привязанной к точке коррекции орбиты небесного тела.

Нетрудно получить оценки величины требуемого импульса скорости, необходимого для увода астероида на заданное расстояние от точки коррекции, принимаемой за исходную. Оценим это расстояние для двух характерных случаев.

В первом из них примем, что орбита проходит через центр Земли, и для избежания удара необходимо получить расстояние увода, равное величине 2R э(коэффициент 2 берется для гарантии). Нетрудно рассчитать, что для выполнения условия избежания удара dn max/R э ≥ 2 необходимо обеспечить величину относительного приращения скорости, равную dV Z/V 0= 85 10 -6. Принимая для оценки требуемого изменения скорости значение V 0= 30 км/с, получим минимальное значение требуемого приращения скорости, равное dV Z= 2,6 м/с.

Во втором случае примем, что необходимо получить отклонение угрожающего тела на ∼ 12 км, т. е. на величину порядка 0,001R э. Это значение соответствует уходу от конкретной зоны резонансного возврата протяженностью ∼ 1 км, реализуемому с большим запасом. Очевидно, что теперь величина необходимого импульса коррекции скорости уменьшится в тысячу раз и составит величину всего лишь порядка нескольких миллиметров в секунду (dV Z= 2,6 мм/с).

Рассматривая результат коррекции орбиты по нормали, можно сразу видеть основной недостаток такой коррекции — ее периодичность и результативность лишь в относительно небольшие интервалы времени, как это следует из характера изменения величины dZ W. Действительно, максимальное значение увода существует практически в течение ∼ 1/6 периода обращения тела, и оно наступит лишь через 1/4 этого периода.

Далее рассмотрим результат приложения импульса скорости по радиусвектору поражающего тела (рис. 10.2).

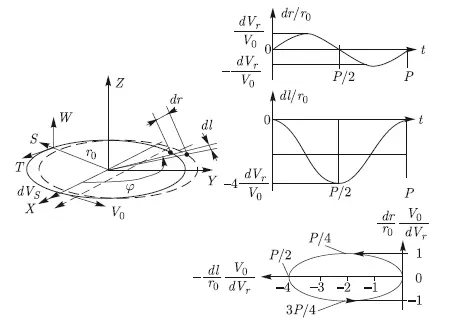
Рис. 10.2. Влияние импульса скорости, приложенного по оси S, на орбиту астероида

Обращаясь к производным, приведенным в работе [Эльясберг, 1965], сразу получаем, что небесное тело будет совершать периодические колебания dr, dl относительно текущего невозмущенного положения по радиус-вектору r (т. е. по координате S) и вдоль орбиты l (практически по координате T):

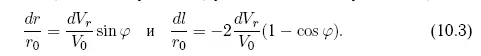
Можно видеть, что и здесь результат коррекции периодичен, но колебания небесного тела возникают уже по двум координатам. Рассматривая отклонение тела в подвижной относительной системе координат, привязанной к текущему первоначальному движению поражающего астероида, можно видеть, что результат коррекции представляет собой эллипс с полуосями dV r/V 0и 2(dV r/V 0) (справа внизу на рис. 10.2).

Таким образом, через 1/4 витка расстояние увода от начальной точки составит √5 (dV r/V 0), причем в дальнейшем, в течение полупериода обращения, эта величина увода будет увеличиваться. Ее максимальное значение будет иметь место через полпериода обращения тела, отсчитываемого от момента коррекции, и составит 4(dV r/V 0). При положительном направлении импульса dV r(от центра орбиты) отклонение по оси T будет направлено в сторону, противоположную движению астероида, т. е. он будет отставать от точки коррекции.

Сравнивая эти результаты с предыдущими, видим, что эффективность коррекции, определяемая по максимальному расстоянию увода, повысилась в 4 раза. Однако и в этом случае периодический характер увода сохраняется. Таким образом, создание импульса коррекции по осям W или S в общем случае полностью задачу увода не решает.