Борис Шустов - Астероидно-кометная опасность: вчера, сегодня, завтра

Рассмотрим результаты коррекции скорости, проводимой по оси Т. И в этом случае результатом коррекции является изменение тех же двух координат в плоскости орбиты, но имеющее уже существенно другой характер. Приложение импульса по оси T изменяет период обращения угрожающего тела на постоянную величину.

Как следствие, по координате T (вдоль орбиты), кроме периодических колебаний, появляется дополнительный уход, линейно нарастающий со временем. Характер изменения текущих координат показан на рис. 10.3, а полные выражения для компонент увода имеют следующий вид:

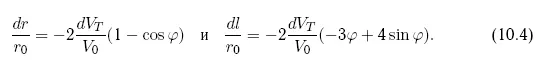
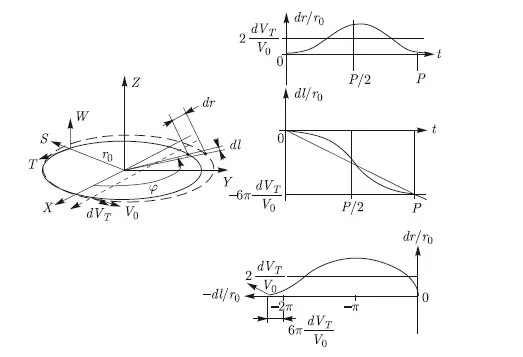
Рис. 10.3. Влияние импульса скорости, приложенного по оси T, на орбиту астероида

Можно видеть, что радиальная компонента увода осталась прежней (правда, с другим знаком), зато у другой компоненты появился линейно нарастающий член, а колебания стали вдвое больше по амплитуде. Тогда средний увод по координате T за один виток будет составлять: dl/R э= 6π(r 0/R э)(dV T/V 0), а сам увод станет пропорционален количеству витков. Любопытно отметить, что при величине отношения dV T/V 0, обеспечивающей целочисленное отношение (1/3)(V 0/dV T) = N в, астероид через N ввитков вернется в ту же точку. Можно видеть, что условием возврата является то, что отношение V 0/dV Tдолжно быть кратно трем.

Этот случай представляет собой своеобразный вариант резонансного возвращения. Правда, практически это произойдет не скоро (как минимум, через десятки тысяч витков орбиты), и по прошествии значительного времени, вследствие возмущений реальной орбиты, возврата в ту же самую точку почти наверняка не произойдет.

Обращаясь к двум последним примерам, рассмотренным выше, получим, что в первом случае требуемый увод можно получить за один виток, создав приращение скорости, равное всего лишь 0,14 м/с. Во втором случае требуемое приращение будет выражаться малыми долями миллиметра в секунду и составит всего лишь 0,14 мм/с.

Сначала рассмотрим результат длительного воздействия постоянной тяги dg W, приложенной по оси W (рис. 10.4).

Можно видеть, что результатом приложения тяги вдоль оси W является поворот плоскости орбиты относительно начальной точки приложения непрерывного воздействия. Заметим, что время приложения тяги принималось равным периоду обращения небесного тела.

Решение линеаризованных уравнений имеет вид:

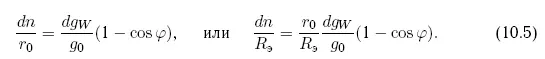
Здесь g 0 — ускорение астероида, вызванное притяжением Солнца: g 0= µ c/r 0 2,

где µ c — гравитационный параметр Солнца, а r 0 — радиус орбиты астероида. Величина dg Wпредставляет собой ускорение тела массой M, создаваемое тягой F. Например, по имеющимся оценкам, масса Апофиса составляет M = 4,6 10 10кг. Схема изменения орбиты под воздействием тяги dg Wпоказана на рис. 10.4.

Ясно, что результат изменения текущих координат тела, как и ранее, оказывается чисто периодическим. Максимальный увод будет иметь место через половину витка орбиты, а его величина составит

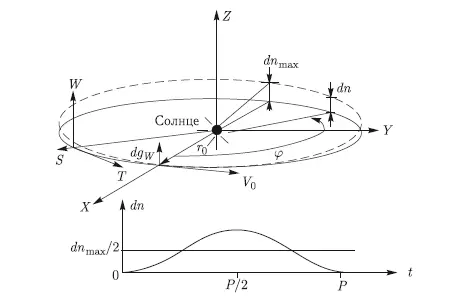
Рис. 10.4. Результат длительного воздействия постоянной тяги dg W, приложенной по оси W

Обратимся к двум выбранным ранее примерам. В первом случае увода на расстояние, равное диаметру Земли, положив dn max/R э= 2, получим, что требуемое значение ускорения dg Wравно: dg W/g 0= (R э/r 0) = 4,25 10 -5. Например, для Апофиса необходимая тяга составит∼ 11,5 кН (килоньютон). Следовательно, такая тяга, приложенная к Апофису в течение полугода, даст изменение текущих координат на диаметр Земли. Во втором случае (увод из зоны резонансного возврата) тяга, прилагаемая также в течение полугода, оказывается в 1000 раз меньше, т. е. составит всего лишь около 11,5 Н.

Перейдем к случаю приложения тяги dg S, длительно действующей по оси S. Это воздействие суммируется с ускорением, создаваемым Солнцем, и, следовательно, изменяет период обращения астероида. При постоянной тяге получаем новую орбиту (рис. 10.5), лежащую в той же плоскости.

Следовательно, изменения координат относительно старых значений описываются формулами

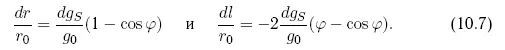
По оси T (вдоль орбиты) появился вековой уход астероида, линейно нарастающий со временем, суммирующийся с периодической составляющей. Величина этого ухода за один виток будет равна dl/r 0=-4π(dg S/g 0). Таким образом, получим удобные выражения для векового ухода за N ввитков и требующегося для этого ускорения:

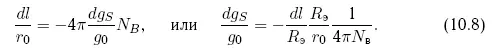
Можно видеть, что приложение длительной по времени тяги по радиус-вектору оказывается более эффективным, чем по нормали. Кроме того, оно тем эффективнее, чем продолжительнее действие тяги. Действительно, в предыдущем случае увод на расстояние dl/R э= 2 требовал тяги (dg W/g 0) = = (R э/r 0), длящейся полвитка. Теперь же величина тяги dg S, прилагаемой в течение той же половины витка и создающей увод dl/R э= 2, оказывается равной (dg S/g 0) = (R э/r 0)(1/π).

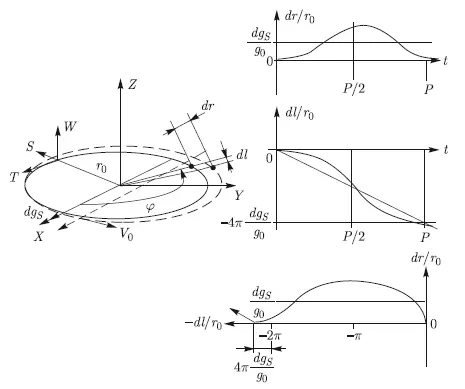
Рис. 10.5. Результат длительного воздействия постоянной тяги dg S, приложенной по оси S

Таким образом, для того же ограниченного времени действия тяги и заданного значения увода изменение направления прилагаемой силы с трансверсального на радиальное дает выигрыш примерно в 3 раза. Увеличив время непрерывного действия до полного витка орбиты, можно при том же значении увода снизить значение тяги вдвое. Дальнейшее увеличение времени непрерывного воздействия тяги позволит еще больше уменьшить ее необходимое значение. Характер увода астероида от начальной точки в относительных координатах показан на рис. 10.5 справа внизу. Это колебания с постоянной амплитудой по радиус-вектору, но приблизительно линейно нарастающие и отстающие вдоль орбиты.

В заключение данного раздела рассмотрим случай непрерывно действующей тяги dg Tпо оси T, которая оказывается наиболее результативной. Вектор тяги, направленный вдоль орбиты, создает ускорение, вызывающее изменение периода обращения угрожающего тела, нарастающее со временем. Теперь орбита будет представлять собой разворачивающуюся спираль (рис. 10.6).