Борис Шустов - Астероидно-кометная опасность: вчера, сегодня, завтра

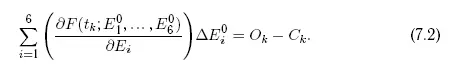
Это так называемое условное уравнение относительно искомых поправок ΔE 0 i.

Частные производные в левых частях условных уравнений могут считаться известными функциями, поскольку они всегда могут быть вычислены с большей или меньшей точностью.

Поскольку число наблюдений при уточнении орбиты почти всегда больше числа уточняемых параметров, то система условных уравнений является избыточной. В общем случае речь может идти лишь о ее приближенном решении. В методе наименьших квадратов решение ищется на основе принципа Лежандра — минимизации суммы квадратов остаточных уклонений. Под остаточными уклонениями ε kпонимаются разности между левыми и правыми частями уравнений (7.2):

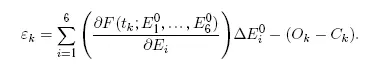
Согласно принципу Лежандра, искомые неизвестные поправки должны минимизировать величину

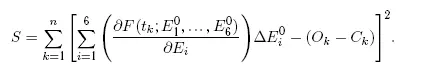
Необходимые условия минимума S как функции переменных ΔE 0 iзаписываются в виде

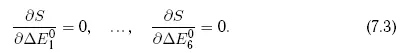
Эти условия образуют систему из шести линейных уравнений относительно шести неизвестных ΔE 0 i(i = 1…, 6). Например, первое из них записывается в виде

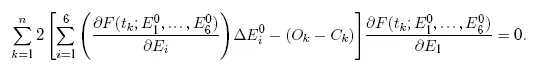
Остальные уравнения записываются аналогично.

Система из шести уравнений (7.3) относительно неизвестных ΔE 0 iназывается нормальной. Использование матричного исчисления позволяет представить нормальную систему и ее решение в компактном виде. Составим матрицу коэффициентов условных уравнений:

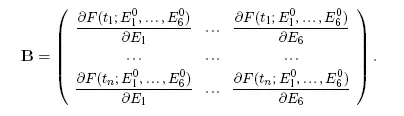
Обозначим также вектор-столбец с компонентами ΔE 0 iкак вектор X, а вектор-столбец правых частей с компонентами O k — C kкак вектор L. В таком случае система условных уравнений запишется в виде

BX = L.

Нормальная система записывается в виде

B TBX = B TL,

где символ T означает транспонирование матрицы (замену строк столбцами и наоборот).

Симметричную матрицу нормальной системы B TB обозначим буквой Q. Решение нормальной системы может быть найдено умножением обеих частей уравнения на матрицу

Q -1= (B TB) -1,

где символом Q -1обозначена матрица, обратная матрице Q (заметим, что матрица Q -1как обратная симметричной матрице, также является симметричной). Произведение обратной матрицы на саму матрицу дает единичную матрицу, вследствие чего решение записывается в виде

X = Q -1B TL. (7.4)

Складывая найденные поправки ΔE 0 iс исходной системой параметров E 0 i, находят исправленную систему. Поскольку при образовании системы условных уравнений мы пренебрегли высшими степенями поправок, то исправленная система элементов не обеспечивает минимального значения суммы квадратов остающихся невязок, хотя обычно уменьшает ее. Для достижения минимума процедуру дифференциального исправления системы элементов приходится повторять до тех пор, пока поправки к элементам не станут достаточно малыми. Найденное таким образом решение называют номинальным .

На практике используется большое число методов решения нормальной системы, в том числе и тот, который, согласно (7.4), основан на обращении матрицы Q, хотя его следует избегать в случае малости определителя матрицы. В теоретическом плане представление решения в виде (7.4) является наглядным и позволяет раскрыть ряд особенностей этого решения. К этому вопросу мы еще вернемся, но прежде рассмотрим вероятностный смысл решения системы условных уравнений методом МНК.

Интересующие нас особенности имеют место только в случае нормального закона распределения ошибок (закона Гаусса):

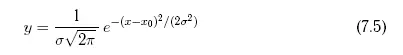
(e — основание натурального логарифма).

Центр распределения определяется значением элемента в номинальном решении, а дисперсии элементов определяются диагональными элементами матрицы Q -1 — обратной матрицы нормальной системы. Иначе говоря, если обозначить среднеквадратичную ошибку элемента E iкак σ i, то

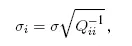
где σ — средняя квадратичная величина остаточных уклонений:

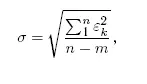
n — число условных уравнений, m — число определяемых неизвестных, в нашем случае 6, Q -1 ii — i-й диагональный элемент обратной матрицы нормальной системы.

Для нормального распределения ошибок элементов орбиты справедливы особенности нормального распределения, в частности то, что вероятность появления ошибки, превышающей утроенное значение среднеквадратичной ошибки элемента, меньше 0,003.

Когда мы говорим об ошибках элементов орбиты, то понимаем при этом возможные отличия элементов от тех значений, которые они имеют в номинальном решении. Таким образом, областью возможных значений для каждого элемента является E i± 3σ i. Каждую возможную орбиту можно представить как точку шестимерного пространства, по осям которого откладываются значения элементов орбит. Рассмотрим малую окрестность некоторой точки этого пространства. Вероятность попадания орбиты в эту окрестность зависит от одновременного попадания шести элементов орбиты в соответствующие элементарные интервалы ΔE i. Мы уже видели, что при нормальном распределении ошибок эти вероятности определяются формулами типа (7.5), т. е.

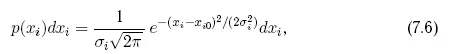
где под x iследует понимать элемент E i, p(x i) — плотность вероятности распределения ошибок соответствующего элемента, σ i — корень квадратный из дисперсии ошибок (среднеквадратичная ошибка i-го элемента).

Предположим ради простоты изложения, что случайные ошибки элементов E iи E jпопарно независимы, т. е. вероятность попадания ошибки элемента E iв некоторый интервал не зависит от ошибки элемента E j. В этом случае ошибки всех элементов являются независимыми в совокупности. Плотность вероятности одновременного попадания шести элементов в достаточно малую окрестность точки (E 1…, E 6) в этом случае выражается как произведение плотностей вероятностей распределения ошибок отдельных элементов: