Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

Рассмотрим частицу с половинным спином , т. е. со значением спина ħ / 2 . Для определенности я буду называть такую частицу электроном , но ею с таким же успехом мог бы быть протон или нейтрон, а также атом подходящего вида. («Частица» может состоять из отдельных частей, если ее можно рассматривать квантовомеханически как единое целое с вполне определенным полным угловым моментом.) Предположим, что наш электрон покоится, и рассмотрим только его спиновое состояние. Пространство квантовомеханических состояний (гильбертово пространство) оказывается в этом случае двумерным , поэтому мы можем выбрать базис, состоящий всего лишь из двух состояний. Я обозначу их |↑)и |↓), чтобы указать, что в состоянии |↑)спин вращается слева направо относительно вертикального направления снизу вверх , в то время как в состоянии |↓)спин вращается слева направо относительно вертикального направления сверху вниз (рис. 6.24).

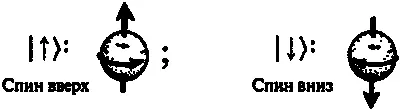
Рис. 6.24.Базис спиновых состояний электрона состоит всего лишь из двух состояний. В качестве них принято выбирать состояния спин вверх и спин вниз

Состояния |↑)и |↓)взаимно ортогональны, и мы считаем их нормализованными ( |↑| 2 и |↓| 2 = 1 ). Любое возможное состояние спина электрона представимо в виде линейной суперпозиции, например, ω |↑) + z |↓), именно этих двух ортонормированных состояний |↑)и |↓), т. е. состояний спин вверх и спин вниз .

Нужно сказать, что в состояниях спин вверх и спин вниз нет ничего особенного. С тем же успехом мы могли бы описывать спин, вращающийся слева направо вокруг любого другого направления, например, слева-направо |→)и противоположного ему справа-налево |←). Тогда (при подходящем выборе комплексных весов) мы получили бы для |↑)и |↓) [155]:

|→)= |↑) + |↓)и |←)= |↑)— |↓).

Это позволяет нам по-новому взглянуть на ситуацию. Любое спиновое состояние электрона есть линейная суперпозиция двух ортогональных состояний |→)и |←),т. е. спинов направо и налево . Можно выбрать какое-нибудь совершенно произвольное направление, например, вектор состояния.

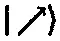
Он также является линейной комбинацией спинов |↑)и |↓)с некоторыми комплексными коэффициентами, скажем,

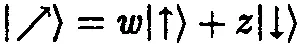
а любое спиновое состояние было бы представимо в виде линейной комбинации этого состояния

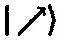
и ортогонального ему [156]состояния

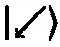
(Заметим, что понятие «ортогональный» в гильбертовом пространстве не обязательно означает «образующий прямой угол с…» в обычном пространстве. Ортогональные вектора состояния в гильбертовом пространстве в данном случае соответствуют диаметрально противоположным направлениям, а не образующим друг с другом прямой угол.)

Каково геометрическое соотношение между направлением в пространстве, определяемым спином

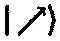
и двумя комплексными числами ω и z ? Так как физическое состояние, задаваемое спином

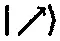
останется неизменным, если мы умножим

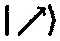
на любое ненулевое комплексное число, то значение имеет только отношение числа z к числу ω . Обозначим это отношение через

q = z / ω .

Тогда q будет обычным комплексным числом за исключением того, что теперь ему разрешено принимать значение q = ∞, чтобы не упускать из рассмотрения ситуацию с ω = 0 , т. е. когда спин направлен вертикально вниз. Если q ≠ ∞, то мы можем представить q как точку на плоскости Аргана, как мы делали это в главе 3. Представим себе, что эта плоскость Аргана расположена горизонтально в пространстве, причем действительная ось направлена вправо в вышеуказанном смысле (т. е. в направлении спинового состояния |→)). Представим теперь сферу единичного радиуса, центр которой совпадает с началом координат плоскости Аргана, а точки 1 , i, — 1 , - i лежат на экваторе этой сферы. Рассмотрим точку, совпадающую с южным полюсом этой сферы, который мы обозначим ∞. Осуществляя проекцию из южного полюса, мы отобразим всю плоскость Аргана на нашу единичную сферу. В результате любая точка q на плоскости Аргана окажется поставленной в соответствие единственной точке q на этой сфере, лежащей на прямой, соединяющей эти две точки с южным полюсом (рис. 6.25).

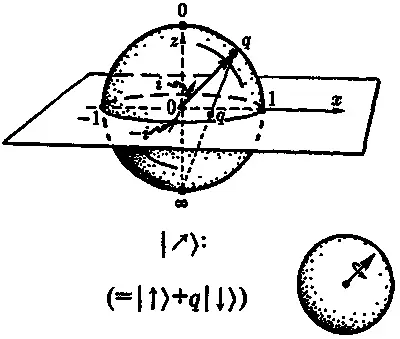
Рис. 6.25.Сфера Римана, представленная как пространство физически различных спиновых состояний частицы со спином 1 / 2 . Сфера Римана стереографически спроецирована из ее южного полюса ( ∞) на плоскость Аргана, проходящую через экватор сферы

Такое соответствие называется стереографической проекцией и обладает многими красивыми геометрическими свойствами (например, сохраняет углы и отображает окружности в окружности). Такая проекция позволяет нам параметризовать точки сферы комплексными числами вместе с ∞, т. е. множеством возможных комплексных отношений q . Сфера, параметризованная таким образом, называется сферой Римана . Геометрический смысл сферы Римана для спиновых состояний электрона состоит в том, что направление спина, задаваемое соотношением

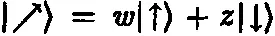
определяется реальным направлением из центра в точку q = z / ω , как показано на изображении сферы Римана. Заметим, что северный полюс соответствует состоянию |↑), задаваемому соотношением z = 0 , т. е. q = 0 , а южный полюс — состоянию |↓), задаваемому соотношением ω = 0 , т. е. q = ∞. Самая правая точка сферы Римана помечена значением q = 1 , что соответствует состоянию |→)= |↑) + |↓)а самая левая точка сферы Римана соответствует q = - 1 , что дает спиновое состояние |←)= |↑)— |↓). Самая дальняя задняя точка сферы Римана помечена значением q = i , соответствующим состоянию |↑) + i |↓), в котором спин направлен прямо от нас, а самая близкая точка сферы Римана помечена значением q = — i , соответствующим состоянию |↑)— i |↓), в котором спин направлен прямо к нам. Произвольная точка, помеченная q , соответствует состоянию |↑) + q |↓).