Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

Исчерпывающее объяснение, почему машина EUC(или UN х 2) на самом деле осуществляет действие, для которого она предназначена, включает в себя некоторые тонкости, и разобраться в нем, может быть, даже труднее, чем понять устройство самой машины — довольно обычная ситуация с компьютерными программами! (Чтобы полностью понять, почему алгоритмические процедуры делают то, что от них ожидается, необходима определенная интуиция. А не являются ли интуитивные прозрения сами алгоритмическими? Это один из вопросов, которые будут для нас важны в дальнейшем.) Яне буду пытаться дать здесь такое объяснение для приведенных примеров EUCили UN х 2. Читатель, шаг за шагом проверив их действие, обнаружит, что я незначительно изменил обычный алгоритм Евклида, чтобы получить более компактную запись в рамках используемой схемы. И все же описание EUCостается достаточно сложным, включая в себя 22 элементарные инструкции для 11 различных внутренних состояний. В основном эти сложности носят чисто организационный характер. Можно отметить, например, что из этих 22 инструкций только 3 в действительности изменяют запись на ленте! (Даже для UN х 2я использовал 12 инструкций, половина из которых меняют запись на ленте.)

Унарная система чрезвычайно неэффективна для записи больших чисел. Поэтому мы по большей части будем использовать вышеописанную двоичную систему. Однако, сделать это напрямую и попытаться читать ленту просто как двоичное число мы не сможем. Дело в том, что мы не имеем возможности сказать, когда кончается двоичное представление числа и начинается бесконечная последовательность нулей справа, которая отвечает пустой ленте. Нам нужен способ как-то обозначать конец двоичной записи числа. Более того, часто нам будет нужно вводить в машину несколько чисел, как, например, в случае с алгоритмом Евклида, когда требуется пара чисел [42]. Но в двоичном представлении мы не можем отличить пробелы между числами от нулей или строчек нулей, входящих в записи этих двоичных чисел. К тому же, помимо чисел нам может понадобиться и запись всевозможных сложных инструкций на той же ленте. Для того чтобы преодолеть эти трудности, воспользуемся процедурой, которую я буду в дальнейшем называть сокращением и согласно которой любая строчка нулей и единиц (с конечным числом единиц) не просто считывается как двоичное число, но замещается строкой из нулей, единиц, двоек, троек и т. д. таким образом, чтобы каждое число в получившейся строчке соответствовало числу единиц между соседними нулями в исходной записи двоичного числа. Например, последовательность

01000101101010110100011101010111100110

превратится в

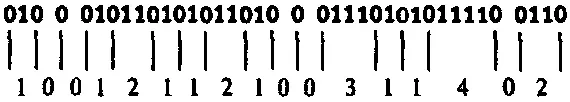
Мы теперь можем считывать числа 2, 3, 4… как метки или инструкции определенного рода. Действительно, пусть 2будет просто «запятой», указывающей на пробел между двумя числами, а числа 3, 4, 5… могли бы по нашему желанию символизировать различные инструкции или необходимые обозначения, как, например, «минус», «плюс», «умножить», «перейти в позицию со следующим числом», «повторить предыдущую операцию следующее число раз», и т. п. Теперь у нас есть разнообразные последовательности нулей и единиц, разделенные цифрами большей величины. Эти последовательности нулей и единиц будут представлять собой обычные числа, записанные в двоичной форме. Тогда записанная выше строка (при замене двоек «запятыми») примет вид:

(двоичное число 1001) запятая (двоичное число 11) запятая….

Используя обычные арабские числа «9», «3», «4», «0» для записи соответствующих двоичных чисел 1001, 11, 100и 0, получаем новую запись всей последовательности в виде: 9, 3, 4 (инструкция 3) 3 (инструкция 4) 0.

Такая процедура дает нам, в частности, возможность указывать, где заканчивается запись числа (и тем самым отделять ее от бесконечной полосы пустой ленты справа), просто используя запятую в конце этой записи. Более того, она позволяет закодировать любую последовательность натуральных чисел, записанных в двоичной системе, как простую последовательность нулей и единиц, в которой для разделения чисел мы используем запятые. Посмотрим, как это сделать, на конкретном примере. Возьмем последовательность

5, 13, 0, 1, 1, 4.

В двоичном представлении она эквивалентна последовательности

101, 1101, 0, 1, 1, 100,

что на ленте можно записать с помощью операции расширения (обратной по отношению к описанной выше процедуре сокращения) как

…000010010110101001011001101011010110100011000…

Такое кодирование легко выполнить, если в исходной двоичной записи чисел провести следующие замены:

0 → 0

1 → 10

, → 110

и после этого добавить бесконечные последовательности нулей с обеих сторон вновь полученной записи. Чтобы сделать более понятной эту процедуру в применении к нашему примеру, разделим полученные двоичные числа пробелами:

0000 10 0 10 110 10 10 0 10 110 0 110 10 110 10 110 10 0 0 110 00.

Я буду называть этот способ представления (наборов) чисел расширенной двоичной записью. (Так, в частности, в расширенной двоичной форме записи число 13 выглядит как 1010010.)

Есть еще одно, последнее, замечание, которое надо сделать в связи с этой системой записи. Это не более, чем техническая деталь, но она необходима для полноты изложения [43]. Двоичная (или десятичная) запись натуральных чисел в некоторой степени избыточна в том смысле, что нули, расположенные слева от записи числа, «не считаются» и обычно опускаются, так что 00110010представляет собой то же самое двоичное число, что и 110010(а 0050 — то же самое десятичное число, что и 50). Эта избыточность распространяется и на нуль, который может быть записан и как 000, и как 00, и, конечно, как 0. На самом деле и пустое поле, если рассуждать логически, должно обозначать нуль! В обычном представлении это привело бы к большой путанице, но в описанной выше системе кодирования никаких затруднений не возникает: нуль между двумя запятыми можно записать просто в виде двух запятых, следующих подряд (''). На ленте такой записи будет соответствовать код, состоящий из двух пар единиц, разделенных одним нулем:

…001101100…

Тогда исходный набор из шести чисел может быть записан в двоичной форме как

101,1101''1,1,100,

и на ленте при кодировании в расширенной двоичной форме мы получим последовательность

…00001001011010100101101101011010110100011000.,

в которой на один нуль меньше по сравнению с предыдущим кодом того же набора.