Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

так что (2g) y = g (gy) . Аналогичным образом он определил:

3 = λ fx. [f (f (fx))] ,

4 = λfх. [f (f (f (fx)))] , и т. д.,

а также

1 = λfх. [fх] и 0 = λ fx.

[x] .

Видно, что 2 Черча больше похоже на «дважды», 3 — на «трижды» и т. д. Значит, действие 3 на функцию f , т. е. 3f равносильно операции «применить f три раза», поэтому 3f при действии на у превращается в

(3f)y = f (f (f (y))) -

Посмотрим, как в схеме Черча можно представить очень простую математическую операцию — прибавление 1 к некоторому числу. Определим операцию

S = λabc. [b ((аb)с)] .

Чтобы убедиться, что S действительно прибавляет 1 к числу в обозначениях Черча, проверим ее действие на 3 :

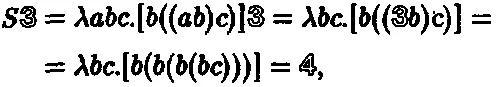
поскольку (3b)с = b (b (bc)) . Очевидно, эта операция с таким же успехом может быть применена к любому другому натуральному числу Черча. (В действительности, операция

λаbс. [(аb)(bс)] приводит к тому же результату, что и S .)

А как насчет удвоения числа? Удвоение числа может быть получено с помощью операции

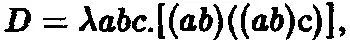
что легко видеть на примере ее действия на 3 :

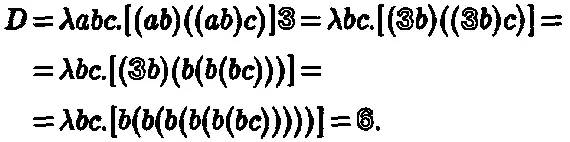
Фактически, основные арифметические операции — сложение, умножение и возведение в степень могут быть определены, соответственно, следующим образом:

А = λfgxy. [((fx)(gx))y],

М = λfgx. [f (gx)],

P = λfg. [fg]

Читатель может самостоятельно убедиться (или же принять на веру), что

(Am) n = m + n ,

(Mm) n = m x n ,

(Pm) n = n m ,

где m и n — функции Черча для двух натуральных чисел, m + n — функция, выражающая их сумму, и т. д. Последняя из этих функций поражает больше всего. Посмотрим, например, что она дает в случае m = 2, n = 3 :

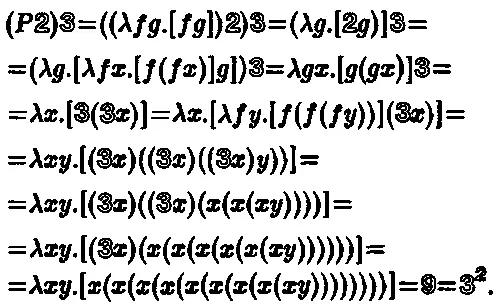
Операции вычитания и деления определяются не так легко (на самом деле нам потребуется соглашение о том, что делать с ( m — n ), когда m меньше n , и с ( m/n ), когда m не делится на n ). Решающий шаг в развитии этого метода был сделан в начале 1930-х годов, когда Клини удалось найти выражение для операции вычитания в рамках схемы Черча! Затем были описаны и другие операции. Наконец, в 1937 году Черч и Тьюринг независимо друг от друга показали, что всякая вычислимая (или алгоритмическая) операция — теперь уже в смысле машин Тьюринга — может быть получена в терминах одного из выражений Черча (и наоборот).

Это воистину замечательный факт, который подчеркивает глубоко объективный и математичный характер понятия вычислимости. На первый взгляд, понятие вычислимости по Черчу не связано с вычислительными машинами. И тем не менее, оно имеет непосредственное отношение к практическим аспектам вычислений. В частности, мощный и гибкий язык программирования LISP включает в себя как существенный элемент основные структуры исчисления Черча.

Как я отмечал ранее, существуют и другие способы определения понятия вычислимости. Несколько позже, но независимо от Тьюринга, Пост предложил во многом сходную концепцию вычислительной машины. Тогда же благодаря работам Дж. Хербранда и Геделя появилось и более практичное определение вычислимости (рекурсивности). X. Б. Карри в 1929 году, и ранее, в 1924, М. Шенфинкель, предложили иной подход, который был отчасти использован Черчем при создании своего исчисления (см. Ганди [1988]). Современные подходы к проблеме вычислимости (такие как машина с неограниченным регистром, описанная Катлендом [1980]) в деталях значительно отличаются от разработанного Тьюрингом и более пригодны для практического использования. Однако понятие вычислимости во всех этих подходах остается неизменным.

Как и многие другие математические идеи, особенно наиболее фундаментальные и красивые, идея вычислимости кажется овеществленной и объективно существующей в платоновском смысле. Именно к этому мистическому вопросу о платоновской реальности математических понятий мы и обратимся в следующих двух главах.

Представим себе, что мы совершаем большое путешествие в некий далекий мир. Назовем его Тор'Блед-Нам. Наша телеметрическая система зарегистрировала сигнал, вывела его на монитор и, отфокусировав изображение, мы увидели следующую картину (рис. 3.1):

рис. 3.1. Первый взгляд на новый мир

Что бы это могло быть? Странного вида насекомое? А может быть, темное озеро с многочисленными втекающими в него ручьями? Или огромный причудливой формы внеземной город, с исходящими в разных направлениях дорогами, которые ведут в расположенные поблизости городки и деревушки? Возможно, это остров — и если это так, то давайте поищем поблизости континент, с которым он связан. Для этого «отойдем назад», т. е. уменьшим увеличение наших приборов раз в 15. И вот — посмотрите-ка — этот новый мир предстал перед нашим взором во всей своей полноте (рис. 3.2):

Рис. 3.2. Общий вид Тор'Блед-Нам. Стрелками

отмечены области, увеличенные изображения которых

даны на рис. 3.1, 3.3 и 3.4

На рис. 3.2 наш «островок» выглядит как маленькая точка под стрелкой «рис. 3.1». Все волокна (ручьи, дороги, мосты?), исходящие из первоначального островка, обрываются, за исключением одного — того, что выходит из внутренней части расположенной справа расщелины, и который, в свою очередь, соединен с объектом гораздо большего размера (он изображен на рис. 3.2). Последний, как нетрудно заметить, подобен первоначальному островку, хотя их формы несколько отличаются. При более подробном рассмотрении «береговой линии» выявляются бесчисленные округлые выступы, края которых, в свою очередь, густо усеяны выступами такой же формы. Каждый маленький выступ соединен в каком-нибудь месте с более крупным, и все вместе они образуют бородавчатую структуру, где более крупные выступы покрыты наростами помельче, те — еще более мелкими и т. д. По мере того, как картина становится все более отчетливой, мы видим мириады мельчайших волокон, исходящих из рассматриваемой структуры. Сами волоконца ветвятся в разных местах, беспорядочно извиваясь. В некоторых частях волокон просматриваются узлы более сложной структуры, неразрешимые при данном увеличении приборов. Ясно, что наш объект — это никакой не остров или континент, и даже не пейзаж. Не исключено, что перед нашим взором чудовищный жук, а то, что мы увидели вначале, — это его детеныш, все еще соединенный с родителем своеобразной волокнистой пуповиной.