Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Мы уже убедились, что в СТО использование светового конуса помогает понять многие явления. В ОТО, в искривленном пространстве-времени, имеет больший смысл представлять его не на всей диаграмме, а в окрестности каждой мировой точки. Это будет локальный световой конус, образованный касательными к световым геодезическим в данной точке. Уравнение светового конуса имеет простой вид – интервал приравнивается нулю: ds = 0.

На рис. 8.2 схематически изображены световые конусы для геометрии Шварцшильда. Предполагая, что движения происходят по радиальным направлениям, диаграмма представлена в координатах r и t . Эти координаты для удаленного наблюдателя в его собственной системе отсчета определяют истинные расстояние и время. Поэтому картина физических явлений, представленная с помощью r и t, – это как раз та картина, которую будет воспринимать удаленный наблюдатель. На рисунке видно, что на значительном удалении «лепестки» конуса расположены под углом 45°, то есть так, как в плоском пространстве-времени. Вертикальные линии соответствуют тем самым зафиксированным (неподвижным) наблюдателям, о которых мы говорили недавно. По мере приближения к черной дыре конус становится все уже, на горизонте он «слипается» и превращается в одну вертикальную линию. Вертикальная линия для удаленного наблюдателя означает, что свет «остановился», его скорость стала «нулевой». Это и означает, что на горизонте все явления замораживаются. Расчет нулевой геодезической показывает, что для удаленного наблюдателя свет никогда не достигнет горизонта.

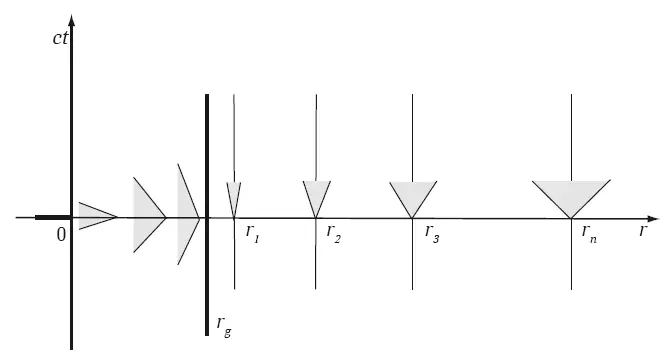
Рис. 8.2. Пространство-время геометрии Шварцшильда в координатах удаленного наблюдателя

Частично такое поведение световых конусов связано с эффектом замедления времени при приближении к гравитирующему центру. Однако, полностью его форма, как мы уже говорили, определяется условием ds = 0, как раз оно определяет «видимую» скорость света для удаленного наблюдателя: v c = c (1 – r g /r ). На значительном удалении от центра скорость близка к c , по мере приближения к центру она уменьшается, а на горизонте, действительно, обращается в нуль. Это прямо связано с формой световых конусов на рис. 8.2. Скорость материальных частиц всегда меньше скорости света (мировая линия физической частицы, находится между створками светового конуса), поэтому их «видимые» предельные скорости тоже уменьшаются при продвижении к центру, и они тоже никогда не достигнут горизонта в координатах r и t . Этот вывод еще раз подтверждает наше описание свободного падения к горизонту с точки зрения удаленного наблюдателя.

Далее продолжим наш мысленный эксперимент , теперь «сожмем» все вещество сферического объекта не только до гравитационного радиуса, а вообще, до «точки» r = 0. То есть все пространство-время будем рассматривать как вакуумное. Формально мы имеем право это сделать, поскольку решение Шварцшильда как раз вакуумное. Обратимся к выражению для метрики. Мы уже отметили, что на горизонте коэффициент g 00при c 2 dt 2обращается в нуль, а коэффициент g 00при dr 2становится бесконечным. Мало того, есть особенность и в «точке» r = 0: здесь, наоборот, g становится равным «минус бесконечности», g 11 – равным нулю. Вспомним, что для «обычного» тела, о котором речь шла в начале параграфа, не возникло никаких особенностей. Далее мы обсудим смысл как особенности на горизонте , так и особенности в центре.

Начнем с горизонта. Вспомним, что в пространстве Минковского физические сущности пространства и времени остаются разными, несмотря на их релятивистский характер. Это проявляется в том, что временная и пространственная части входят в выражение для интервала с разными знаками: первая – со знаком «плюс», вторая – со знаком «минус». Это так и есть для решения Шварцшильда на удалении от горизонта (в «регулярной» области пространства). Временная часть, определяемая коэффициентом g 00при c 2 dt 2, действительно, положительна, а пространственная , определяемая коэффициентом g 11при dr 2, – отрицательна.

А что будет под горизонтом? Там ситуация изменилась: в выражении для интервала мы должны учесть r < r g, тогда коэффициент g 00при c 2 dt 2становится отрицательным , а коэффициент g 11при dr 2становится, наоборот, – положительным . А это, как только что мы

обсудили, означает, что под горизонтом координата t становится пространственной, а координата r – временной! Теперь, учитывая этот факт, построим световые конусы под горизонтом. Поскольку на диаграмме координаты r и t поменяли смысл, световые конусы как бы лягут на бок, с внутренней стороны на горизонте их створ равен 180°, затем приближаясь к центру r = 0, створ уменьшается. Как всегда, мировая линия реальной физической частицы должна быть внутри створа светового конуса. Наконец, при r = 0 лепестки конусов окончательно «слипаются», как показано на рис. 8.2. Расположение и форма световых конусов под горизонтом говорят о двух вещах. Первое, действительно, ни лучи света, ни какая материальная частица не могут покинуть горизонт и область под ним; второе, все частицы и свет, оказавшись под горизонтом, неминуемо достигнут начала координат при r = 0. Действительно, створ конуса всегда направлен к линии r = 0.

Мы видим, что под горизонтом нет препятствий для движения частиц, хотя и выглядит это несколько необычно. С другой стороны, сигналы извне не могут преодолеть горизонт. Происходит разрыв мировых линий световых лучей и падающих частиц. Самое время обсудить особенность на горизонте. Попытаемся понять, что на горизонте и в его окрестности происходит в реальности.

Придется вернуться к истокам ОТО и вспомнить, что основной характеристикой пространства-времени является его искривление (кривизна), которое определяется тензором кривизны Римана. Но вычисление компонент тензора Римана на горизонте и в его окрестности ничего необычного не обнаруживает. До горизонта, на горизонте и под ним кривизна не испытывает никаких разрывов, ведет себя вполне плавно, постепенно увеличиваясь по мере приближения к центру. Дело в том, что координаты удаленного наблюдателя (а это координаты плоского пространства-времени), в которых и записано решение Шварцшильда, не вполне годятся для описания явлений в окрестности горизонта. Это значит, что нужно найти координаты, которые не имели бы этого дефекта.