Ричард Фейнман - 9. Квантовая механика II

Трудность с электроном состоит в том, что вы не можете по­местить в одно и то же состояние больше одного электрона. Поэтому очень долго считалось, что волновая функция уравне­ния Шредингера никогда не будет иметь макроскопического представления, подобного макроскопическому представлению амплитуды для фотонов. Но теперь стало ясно, что явление сверх­проводимости представляет именно такой случай.

§ 5. Сверхпроводимость

Вы знаете, что очень многие металлы ниже определенной температуры (температура у каждого металла своя) становятся сверхпроводящими. Если вы как следует снизите температуру то металлы начинают проводить электричество без всякого соп­ротивления. Это явление наблюдалось у очень многих металлов, но не у всех, и теория этого явления причинила немало хлопот. Понадобилось довольно долгое время, чтобы разобраться, что происходит внутри сверхпроводников, и я опишу здесь только то, что будет нужно для наших нынешних целей. Оказывается, что из-за взаимодействия электронов с колебаниями атомов в решетке возникает слабое эффективное притяжение между электронами. Грубо говоря, электроны в итоге взаимодействия образуют связанные пары.

Известно также, что каждый отдельный электрон яв­ляется ферми-частицей. Но связанная пара уже будет вести себя как бозе-частица, потому что, если я переставляю местами два электрона в паре, я дважды меняю знак волновой функции, а это означает, что я ничего не меняю. Пара является бозе-частицей.

Энергия спаривания (энергия притяжения электронов) очень-очень слаба. Незначительной температуры достаточно, чтобы тепловое возбуждение разбросало электроны и обратило их в «нормальные» электроны. Но если снизить температуру доста­точно сильно, то эти электроны сделают все от них завися­щее, чтобы прийти в самое наинизшее состояние, и уж тогда-то действительно разберутся попарно.

Мне не хотелось бы, чтобы вы вообразили, будто пары и впрямь скреплены очень тесно, словно точечные частицы. В действительности, именно в этом пункте лежала наибольшая труд­ность в понимании этого явления на первых порах. Два элек­трона, образующие пару, в действительности расходятся на заметные расстояния; и среднее расстояние между парами мень­ше размера отдельной пары. Несколько пар одновременно за­нимают один и тот же объем. Объяснение причины образования электронами в металле пар и оценка энергии, выделяемой при образовании пар, стало триумфом современной науки. Этот фун­даментальный факт в явлении сверхпроводимости впервые разъяснен в теории, созданной Бардином, Купером и Шриффером. Но не это будет темой нашего семинара. Мы попросту примем как данное представление о том, что электроны так или иначе действуют попарно, что можно считать, что эти пары ведут себя более или менее как частицы и что поэтому можно гово­рить о волновой функции «пары».

Уравнение Шредингера для пары более или менее похоже на (19.3). Единственная разница состоит в том, что заряд q бу­дет удвоенным зарядом электрона. Кроме того, мы не знаем инер­ции (или эффективной массы) пары в кристаллической решетке, поэтому неизвестно, какое число поставить вместо т. Не сле­дует также считать, что если перейти к очень высоким частотам (или коротким волнам), то форма уравнения останется правиль­ной, ведь кинетическая энергия, которая отвечает очень резко меняющимся волновым функциям, может стать столь большой, что разрушит пары. При конечных температурах в соответствии с теорией Больцмана всегда встречается сколько-то разрушенных пар. Вероятность того, что пара разрушится, пропорциональна ехр(- E пары /kT). He связанные попарно электроны называются «нормальными» и движутся по кристаллу обычным образом. Я буду, однако, рассматривать только случай истинно нулевой температуры или, во всяком случае, пренебрегу усложнениями, вызываемыми теми электронами, у которых нет пары.

Раз пары электронов—это бозоны, то когда множество их собирается в одном состоянии, амплитуда перехода других пар в то же состояние становится особенно велика. Значит, почти все пары должны скопиться при наинизшей энергии в точности в одинаковом состоянии, сбежать кому-либо из них в другое состояние очень нелегко. У каждой пары амплитуда того, что она перейдет в занятое состояние в Ц n раз больше, чем в не­занятое (где хорошо известный фактор Ц n определяется насе­ленностью n наинизшего состояния). Значит, мы вправе ожи­дать, что все пары будут двигаться в одном состоянии.

Как же тогда будет выглядеть наша теория? Я обозначу че­рез y волновую функцию пары в наинизшем энергетическом со­стоянии. Однако из-за того, что yy* окажется пропорциональ­ным плотности заряда r, я с равным правом могу записать y как квадратный корень из плотности заряда, умноженный на некоторый фазовый множитель

где r и q — действительные функции от r.(В таком виде можно, конечно, записать любую комплексную функцию.) Что мы под­разумеваем, говоря о плотности заряда,— это ясно, но каков физический смысл фазы 9 волновой функции? Ну что же, да­вайте поглядим, что получится, если мы подставим y (r) в (19.12) и выразим плотность тока через эти новые переменные r и q. Это простая замена переменных, и, не повторяя всех выкладок, я приведу результат:

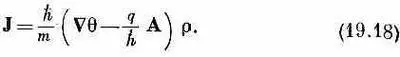
Поскольку и плотность тока и плотность заряда имеют для сверхпроводящего электронного газа прямой физический смысл, то и r и q — вполне реальные вещи. Фаза столь же наблюдаема, как и r: это часть плотности тока J. Абсолютная фаза ненаблю­даема, но если градиент фазы известен во всех точках, то фаза известна с точностью до константы. И если вы определите по своему желанию фазу в одной точке, то во всех остальных точ­ках она уже определится сама собой.

Кстати заметим, что уравнение для тока можно проанализи­ровать и изящнее, если представить себе, что плотность тока и впрямь совпадает с произведением плотности заряда на ско­рость тока электронной жидкости, т. е. что J=r v. Тогда (19.18) равнозначно уравнению

Мы замечаем, что в mv -импульсе есть две части: одна связана с векторным потенциалом, а другая с поведением волновой функции. Иными словами, величина h Сq— это как раз то, что мы называли р -импульсом.