Ричард Фейнман - 8. Квантовая механика I

Однако раз нас интересуют частоты, то надо подставить k=w/c, и мы получаем

Но здесь возникает одно усложнение. Если мы говорим о собственных колебаниях электромагнитной волны, то каж­дому данному волновому вектору kможет соответствовать любая из двух поляризаций (перпендикулярных друг другу). Поскольку эти собственные колебания независимы, то нужно (для света) удвоить их число. И мы имеем

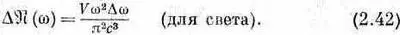
Мы показали уже [см. (2.33)], что каждое собственное коле­бание (мода, тип колебаний, «состояние») обладает в среднем

энергией

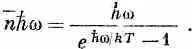
Умножая это на число собственных колебаний, мы полу­чаем энергию D Е. которой обладают собственные колебания лежащие в интервале Dw

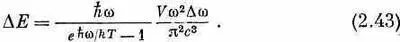
Это и есть закон для спектра частот излучения абсолютно черного тела, найденный нами уже однажды в гл. 41 (вып. 4). Спектр этот вычерчен на фиг. 2.10.

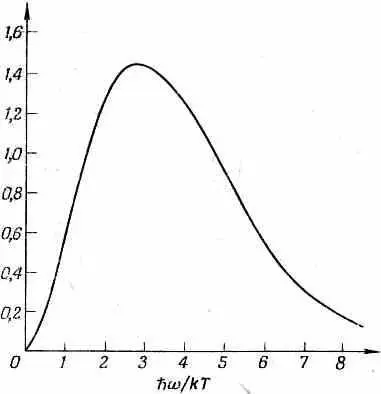
Фиг. 2.10. Спектр частот излучения в полости при тепловом равновесии (спектр «абсолютно чер­ного тела»).

На оси ординат отложена величина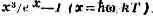

отличающаяся от dE/dw постоянным множителем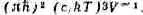

Вы теперь видите, что ответ зависит от того факта, что фотоны являются бозе-частицами — частица­ми, имеющими тенденцию собираться всем вместе в одном и том же состоянии (амплитуда такого поведения велика). Бы помните, что именно Планк, изучавший спектр абсолютно чер­ного тела (который представлял загадку для классической фи­зики) и открывший формулу (2.43), положил тем самым начало квантовой механике.

§ 6. Жидкий гелий

Жидкий гелий при низких температурах обладает рядом странных свойств, на подробное описание которых у нас, к со­жалению, не хватает времени. Многие из них просто связаны с тем, что атом гелия — это бозе-частица. Одно из этих свойств— жидкий гелий течет без какого бы то ни было вязкого сопротив­ления. Это в действительности та самая «сухая» вода, о которой мы говорили в одной из прежних глав (при условии, что ско­рости достаточно низки). Причина здесь вот в чем. Чтобы жи­дкость обладала вязкостью, в ней должны быть внутренние поте­ри энергии; надо, чтобы одна из частей жидкости могла двигаться не так, как оставшаяся жидкость. Это означает, что должна быть возможность выбивать некоторые атомы в состояния, отличные от тех, в которых пребывают другие атомы. Но при достаточно низких температурах, когда тепловое движение становится очень слабым, все атомы стремятся попасть в одни и те же ус­ловия. Так, если некоторые из них движутся в одну сторону, то и все атомы пытаются двигаться все вместе таким же образом. Это своего рода жесткость по отношению к движению, и такое движение трудно разбить на неправильные турбулентные части, как это было бы, скажем, с независимыми частицами. Итак, в жидкости бозе-частиц есть сильное стремление к тому, чтобы все атомы перешли в одно состояние,— стремление, представ­ляемое множителем Ц(n+1), полученным нами ранее. (А в бутылке жидкого гелия n, конечно, очень большое число!) Это движение не происходит при высоких температурах, потому что тогда тепловой энергии хватает на то, чтобы перевести разные атомы во всевозможные различные высшие состояния. Но при достаточном понижении температуры внезапно насту­пает момент, когда все атомы гелия стремятся оказаться в одном и том же состоянии. Гелий становится сверхтекучим. Кстати, это явление возникает лишь у изотопа гелия с атомным весом 4. Отдельные атомы изотопа гелия с атомным весом 3 суть ферми-частицы, и жидкость здесь самая обычная. Поскольку сверх­текучесть бывает лишь у Не 4, то со всей очевидностью этот эффект квантовомеханический, вызываемый бозевской приро­дой a-частицы.

§ 7. Принцип запрета

Ферми-частицы ведут себя совершенно иначе. Посмотрим, что произойдет, если мы попытаемся поместить две ферми-частицы в одно и то же состояние. Вернемся к нашему первона­чальному примеру и поинтересуемся амплитудой того, что две идентичные ферми-частицы рассеются в почти одинаковом на­правлении. Амплитуда того, что частица а пойдет в направ­лении 1, а частица b — в направлении 2, есть

<1| a >.<2| b >,

тогда как амплитуда того, что направления вылетающих частиц обменяются местами, такова:

<2| а ><1| b>.

Раз мы имеем дело с ферми-частицами, то амплитуда процесса является разностью этих двух амплитуд:

<1| а ><2| b >-<2| а ><1| b >. (2.44)

Следует сказать, что под «направлением 1» мы подразумеваем, что частица обладает не только определенным направлением, но и заданным направлением своего спина, а «направление 2» почти совпадает с направлением 1 и отвечает тому же направ­лению спина. Тогда <1| а > и <2| а > будут примерно равны. (Этого могло бы и не быть, если бы состояния 1 и 2 вылетающих частиц не обладали одинаковым спином, потому что тогда по каким-то причинам могло бы оказаться, что амплитуда зависит от направления спина.) Если теперь позволить направлениям 1 и 2 сблизиться друг с другом, то полная амплитуда в уравне­нии (2.44) станет равной нулю. Для ферми-частиц результат много проще, чем для бозе-частиц. Просто абсолютно невоз­можно, чтобы две ферми-частицы, например два электрона, оказались в одинаковом состоянии. Вы никогда не обнаружите два электрона в одинаковом положении и со спинами, направленными в одну сторону. Двум электронам невозможно иметь один и тот же импульс и одно и то же направление спина. Если они оказываются в одном и том же месте или в одном и том же состоянии движения, то единственное, что им остается,— это завертеться навстречу друг другу.

Каковы следствия этого? Имеется множество замечатель­ных эффектов, проистекающих из того факта, что две ферми-частицы не могут попасть в одно и то же состояние. На самом деле почти все особенности материального мира зависят от этого изумительного факта. Все разнообразие, представленное в периодической таблице элементов, в основе своей является следствием только этого правила.