Ричард Фейнман - 8. Квантовая механика I

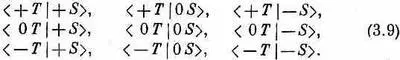
Некоторые соотношения между этими амплитудами мы сразу можем себе представить. Во-первых, согласно нашим определениям, квадрат модуля

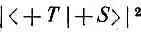
— это вероятность того, что атом, бывший в состоянии ( + S ), придет в состояние ( +Т ) . Такие квадраты удобнее писать в эквивалентном виде

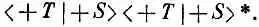
В тех же обозначениях число

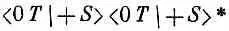
дает вероятность того, что частица в состоянии (+ S ) перей­дет в состояние (0 T ), а

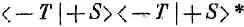
— вероятность того, что она перейдет в состояние (- Т). Нонаши приборы устроены так, что каждый атом, входящий в прибор Т, должен быть найден в каком-то одном из трех со­стояний прибора Т', — атомам данного сорта нет других путей. Стало быть, сумма трех только что написанных вероятностей должна равняться единице. Получается соотношение

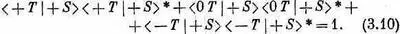
Имеются, конечно, еще два таких же уравнения для случаев, когда вначале было состояние (0 S) или (- S). Их очень легко написать, так что мы переходим к другим общим вопросам.

§ 3. Последовательно соединенные фильтры Штерна — Герлаха

Пусть у нас есть атомы, отфильтрованные в состояние (+ S ), которые мы затем пропустили через второй фильтр, переведя, скажем, в состояние (О Т), а затем — через другой фильтр (+ S ). (Обозначим его S ', чтобы не путать с первым фильтром S .) Вспомнят ли атомы, что они уже раз были в со­стоянии (+ S )? Иначе говоря, мы ставим такой опыт:

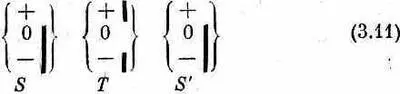
и хотим знать, все ли атомы, прошедшие сквозь Т, пройдут и сквозь S'. Нет. Как только они пройдут фильтр Т, они сразу же позабудут о том, что, входя в Т, они были в состоянии (+ S ). Заметьте, что второй прибор S в (3.11) ориентирован в точности так же, как первый, так что это по-прежнему фильтр типа S. Состояния, выделяемые фильтром S', — это, конечно, все те же (+S), (0S) и (-S).

Здесь существенно вот что: если фильтр Т пропускает толь­ко один пучок, то та доля, пучка, которая проходит через второй фильтр S, зависит только от расположения фильтра Т и совер­шенно не зависит от того, что было перед ним. Тот факт, что те же самые атомы однажды уже были отсортированы фильтром S , никак и ни в чем не влияет на то, что они будут делать после того, как прибор Т снова отсортирует их в чистый пучок. От­сюда следует, что вероятность перейти в те или иные состояния для них одна и та же безотносительно к тому, что с ними слу­чалось до того, как они угодили в прибор Т, Для примера сравним опыт (3.11) с опытом

в котором изменилось только первое S. Пусть, скажем, угол a (между S и Т) таков, что в опыте (3.11) треть атомов, прошед­ших сквозь Т, прошла также и через S'. В опыте (3.12), хоть в нем, вообще говоря, через Т пройдет другое число атомов, но через S' пройдет та же самая, часть их — одна треть.

Мы можем на самом деле показать, опираясь на то, чему мы научились раньше, что доля атомов, которые выходят из Т и проходят через произвольный определенный фильтр S', зависит лишь от Т и S', а не от чего бы то ни было происходившего ра­нее. Сравним опыт (3.12) с

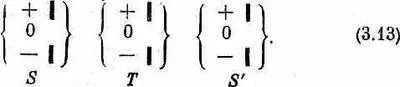
Амплитуда того, что атом, выходящий из S, пройдет и сквозь Т, и сквозь 6", в опыте (3.12) равна

<+S |0 T>< 0 T |0 S>.

Соответствующая вероятность такова:

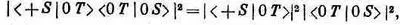
а вероятность в опыте (3.13)

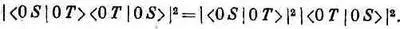
Их отношение

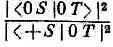
зависит только от Т и S' и совсем не зависит от того, какой пу­чок (+ S ), ( 0 S) или (- S) был отобран в S. (Абсолютные же количества могут быть большими или меньшими, смотря по тому, сколько прошло через Т.) Мы бы получили, конечно, аналогичный результат, если бы сравнили вероятности того, что атомы перейдут в плюс- или минус-состояние (по отноше­нию к S '), или отношения вероятностей перейти в нуль- или минус-состояние.

Но раз эти отношения зависят только от того, какой пучок может пройти сквозь Т, а не от отбора, выполненного первым фильтром S, то становится ясно, что тот же результат получил­ся бы, если бы последний прибор даже не был фильтром S. Если в качестве третьего прибора (назовем его R) мы используем прибор, повернутый относительно Т на некоторый произволь­ный угол, то все равно увидим, что отношения типа

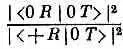
не зависят от того, какой пучок проник через первый фильтр S.

§ 4. Базисные состояния

Эти результаты иллюстрируют один из основных принципов квантовой механики: любая атомная система может быть раз­делена процессом фильтрования на определенную совокуп­ность того, что мы назовем базисными состояниями, и будущее поведение атомов в любом данном отдельном базисном состоя­нии зависит только от природы базисного состояния — оно не зависит от предыдущей истории. Базисные состояния за­висят, конечно, от примененного фильтра; например, три со­стояния (+ Т ), (0 Т) и (- Т)— это одна совокупность базисных состояний, а три состояния (+ S ), (0 S ) и (- S) — другая. Возможностей сколько угодно, и ни одна не хуже другой.

Необходимо быть осторожным, утверждая, что мы рас­сматриваем хорошие фильтры, которые действительно создают «чистые» пучки. Если, скажем, наш прибор Штерна — Герлаха недостаточно хорошо отделяет пучки друг от друга, то Мы не можем произвести полного разделения на базисные состояния. Мы можем проверить, есть ли у нас чистые базисные состояния, посмотрев, смогут ли пучки опять расщепиться еще одним таким же фильтром. Если, например, имеется чистое состояние (+ T ), то все атомы пройдут через