Александр Филиппов - Многоликий солитон

Общие решения нелинейного уравнения маятника можно выразить через так называемые эллиптические функции Якоби (мы их уже упоминали, когда говорили о форме нелинейных волн, (рис. 2.2).

Замечательно, однако, что движение, соответствующее сепаратрисе фазовой диаграммы, можно записать с помощью элементарных функций. Геометрический вывод этого решения приведен в Приложении, где показано, что для решения φ( t ), обращающегося в нуль при t = 0, выполнено простое соотношение

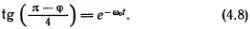
Общее решение уравнения (4.6) можно получить отсюда сдвигом начала отсчета времени, т. е. заменой в формуле (4.8) t на t 0. Чтобы хорошо понять это решение, выразим φ непосредственно через t :

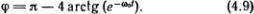
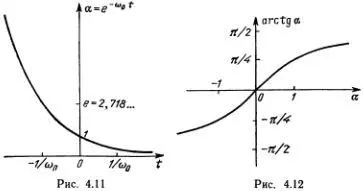
График этой функции легко построить, вспомнив, как выглядят графики показательной функции и aгctg (рис. 4.11, 4.12). Когда t растет от - 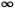до + 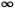, α убывает от + 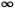до 0.

При этом aгctg α пробегает значения от π/2 до 0, а φ меняется от -π до +π. Таким образом, написанное решение соответствует сепаратрисе, идущей из точки -π в точку +π.

Вспоминая, что φ удовлетворяет уравнению (4.6), после несложных тригонометрических преобразований можно найти, что

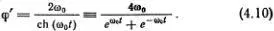
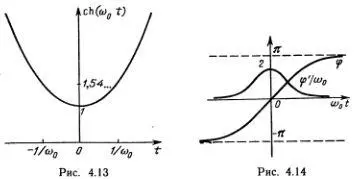
Здесь мы ввели в употребление так называемый гиперболический косинус

ch(ω 0 t ) = 1/2(e ω 0 t + е -ω 0 t ),

часто встречающийся в теории солитонов. (Геометрическое определение этой и других гиперболических функций можно найти в Приложении.) Легко построить график этой функции (рис. 4.13).

Теперь легко получить графики φ( t ) и φ'(t), описывающие особое движение маятника (рис. 4.14). Эти две замечательные и простые функции стоит как следует изучить и запомнить.

Качественный характер изученных нами движений маятника полезно изучить на простых опытах. Проще всего сделать это с помощью обычного велосипедного колеса. Перевернув велосипед, можно сделать из переднего колеса неплохой маятник, способный совершать колебательные и вращательные движения. Для этого прикрепим на ободе кусочек пластилина или какой-либо иной грузик. Если колесо не сбалансировано, лучше его сначала сбалансировать, так чтобы оно могло покоиться в любом положении. Внешняя сила, действующая на колесо, определяется только дополнительным грузиком, а в движении участвует вся его масса.

Чтобы оценить период движения колеса, приближенно заменим его однородным тонким обручем с радиусом, примерно равным расстоянию l от центра до внутренней части обода, и с массой, примерно равной массе всего колеса М . Приложенная сила равна - mg sin φ, а ее момент равен mgl sin φ, где m — масса дополнительного грузика, а φ — угол отклонения его от вертикали, отсчитываемый точно так же, как и для обычного маятника. Мысленно разделим обруч на n одинаковых маленьких частей. Если к каждой приложить силу -(1/n) mg sin φ, направленную по касательной к обручу, то приложенный полный момент силы равен - mgl sin φ, так что такое «разделение» внешней силы допустимо. Для каждой маленькой части легко написать уравнение движения

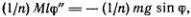
поскольку все части движутся как целое и их ускорения одинаковы. Таким образом, мы получили уравнение, совпадающее с уравнением движения обычного маятника φ" = -ω 0 2sin φ, но теперь ω 0 2 = mg/Ml . Этот вывод не зависит от сделанных приближений, приближенным получилось лишь выражение для ω 0 2(в точной формуле вместо Ml надо подставить I/l , где I — момент инерции колеса; для обруча I = Ml 2 ).

На этом простом приборе можно изучить все движения, которые были рассмотрены выше. Нужно только помнить, что трение приводит к затуханию колебаний, закон сохранения энергии становится приближенным и фазовый портрет маятника при наличии трения существенно изменяется (попробуйте показать, что для линейного маятника с трением окружности на фазовой плоскости переходят в спирали, накручивающиеся на точку φ = 0, φ' = 0).

На велосипедном колесе легко установить изохронность малых и неизохронность больших колебаний. Нетрудно также найти зависимость периода колебаний от амплитуды и установить качественный характер любых движений.

Однако построить экспериментальные графики движений не очень просто. Самый удобный способ — сделать киносъемку движений колеса, но это уже достаточно дорогостоящий опыт. Замечательно, что зависимость угла от времени для самых разных движений можно определить на опыте с помощью очень простой системы, которая, на первый взгляд, не имеет ничего общего с маятником.

Возьмем тонкую и достаточно длинную стальную проволочку. Она должна легко гнуться без заметной остаточной деформации. Если ее положить на стол и слегка сжать на концах, она примет форму полусинусоиды, как указано в верхней части рис. 4.15.

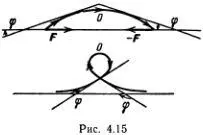
Проведем касательные к получившейся кривой и будем отсчитывать угол φ, как указано на рисунке. Длину дуги s на кривой будем отсчитывать от точки О , причем слева s 0, а справа s 0. Если на проволочке сделать петельку, как указано в нижней части рис. 4.15, то угол будет принимать значения от -π до +π, если считать проволочку бесконечно длинной. При этом зависимость φ от s описывается формулой (4.9), в которой вместо t надо подставить s , а ω 0определяется силой F , действующей на проволочку. Если проволочка бесконечно длинная, то петелька может располагаться в любом месте, она может свободно перемещаться вдоль проволочки. Эта петелька и есть простейшая модель солитона. Назовем этот солитон «ручным».

С движением маятника связаны любые формы изгиба проволочки. Каждой зависимости φ( s ) от s можно поставить в соответствие некоторое движение маятника. Эта замечательная аналогия называется аналогией Кирхгофа в честь открывшего ее знаменитого немецкого физика Густава Кирхгофа (1824—1887) *). На самом деле он нашел гораздо более широкую аналогию между состояниями деформированных упругих тел и движениями твердого тела. К сожалению, о ней сегодня совершенно незаслуженно забыли. Мы немного поговорим о ней после того, как познакомимся с солитоном Френкеля.