Александр Филиппов - Многоликий солитон

Примерно по такой же схеме велись вычисления в небесной механике (невозмущенное движение — это движение по кеплеровым эллиптическим орбитам). Лагранж и особенно Лаплас выполнили большие и трудоемкие вычисления возмущенных движений планет, на основании которых можно было определить точные положения планет в далеком прошлом и будущем. Применяя их методы, Адамс и Леверье впоследствии обнаружили отклонение орбиты Урана от рассчитанных значений и объяснили это явление возмущающим влиянием новой, неизвестной планеты Нептун.

В дальнейшем А. Пуанкаре и замечательный русский математик Александр Михайлович Ляпунов (1857—1918) чрезвычайно усовершенствовали и обобщили методы возмущений. Хотя они в основном интересовались задачами небесной механики, созданные ими методы оказались столь общими, что их легко было приспособить к решению совсем других нелинейных задач физики и техники. Когда примерно 50 лет назад Мандельштам и Андронов начали применять методы Ляпунова и Пуанкаре в нелинейной радиофизике, они были немало поражены тем, сколь эффективны методы небесной механики при расчете, например, работы лампового генератора. С тех пор область применения этих методов постоянно расширялась.

Примерно в то же время Николай Митрофанович Крылов (1879—1955) и Николай Николаевич Боголюбов разработали новые методы теории возмущений в нелинейной механике, позволяющие описывать не только периодические, но и гораздо более сложные движения нелинейных систем. Эти методы были применены Н. Н. Боголюбовым к описанию хаотических движений в системах, состоящих из очень большого числа частиц. В последние годы, в особенности под влиянием идей А. Н. Колмогорова и В. И. Арнольда, началось объединение качественных и количественных методов исследования нелинейных систем. Все это привело к замечательному расцвету нелинейной механики, которая теперь с успехом применяется в самых разных науках и сыграла огромную роль в развитии теории солитонов.

Продолжим разбор движений маятника, следуя по пути, подсказываемому физической и отчасти геометрической интуицией. Ясно, что фазовые траектории можно нарисовать для движения маятников с любой энергией. Совокупность всех возможных фазовых траекторий составляет фазовый портрет. По этому портрету легко получить наглядное представление о всевозможных движениях.

Чтобы научиться рисовать и без труда понимать фазовые портреты, рассмотрим сначала совсем простые задачи. Пусть точка равномерно движется по прямой и в начальный момент t = 0 ее координата s равна нулю, так что s = v 0t . График этого движения — прямая линия с наклоном, пропорциональным скорости (рис. 4.8, α).

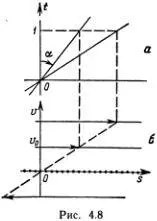
Если на вертикальной оси графика 1 см соответствует 1 с времени, а 1 см по горизонтали соответствует 1 см пути, то скорость, очевидно, равна tg α см/с. Дальше мы не будем упоминать об этом соглашении и с производными величинами будем обращаться точно так же (на оси скорости 1 см соответствует скорость 1 см/с и т. д.). Отрицательным значениям угла отвечают движения в отрицательном направлении по оси Os (рис. 4.8, б).

Нетрудно нарисовать любую фазовую траекторию. Это просто прямые, параллельные горизонтальной оси Os и пересекающие вертикальную ось в точке, соответствующей значению скорости, равному v 0. Когда скорость положительна, изображающая точка А пробегает фазовую траекторию слева направо, при отрицательной скорости — в обратном направлении. Если s = s 0+ v 0t, то график движения не проходит через точку О, но фазовая траектория такого движения совпадает с фазовой траекторией движения s = v 0t. Это, конечно, легко проверить, но на самом деле это должно быть очевидным, так как фазовые траектории не зависят от момента t 0, в котором мы начинаем отсчет времени.

Если точка покоится, то на графике движения ей соответствует прямая, параллельная оси времени, т. е. s = s 0и α = 0. На фазовой диаграмме этой прямой соответствует точка s = s 0на оси Os , т. е. точка ( s, v ) = ( s 0, 0). При разных значениях s 0эти точки заполняют всю ось Os . Каждую точку оси Os нужно рассматривать как отдельную фазовую траекторию.

Таким образом, фазовые траектории точки, движущейся равномерно по прямой, — это прямые, параллельные оси Os , а также точки оси Os . Через каждую точку фазовой плоскости ( s, v ) проходит только одна фазовая траектория, если договориться, что выбор начала отсчета времени t 0несуществен (т. е. важно лишь, какую кривую пробегает изображающая точка). Чтобы больше не возвращаться к этому, можно, как это делалось и раньше, условиться, что s = 0 при t = 0 , а остальные движения получать сдвигом начала отсчета времени.

В качестве упражнения постройте фазовые диаграммы равномерно ускоренных движений грузика, падающего с высоты h или подбрасываемого вверх. Точка О на фазовой диаграмме представляет фазовую траекторию лежащего на земле грузика. Вообще, такие точки на фазовых диаграммах называются точками покоя . В самом нижнем положении наш грузик покоится устойчиво, иными словами, точка на фазовой диаграмме — устойчивая точка покоя . Если грузик слегка подбросить, он вернется назад. Дальнейшее движение грузика зависит от его устройства как реальной физической системы. Если грузик — модель упругого мячика, падающего на асфальт, то он будет отскакивать, пока вся его энергия не перейдет в тепло (попробуйте нарисовать фазовые траектории этих движений). Если же уронить на пол кусочек пластилина, то он останется в нижнем положении (какова фазовая траектория в этом случае?).

Точки покоя на фазовом портрете равномерно движущегося грузика, наоборот, неустойчивы. Если сообщить грузику небольшой импульс, то он начнет равномерно двигаться и в конце концов уйдет сколь угодно далеко от исходного положения. На фазовом портрете это будет выглядеть так, что точка ( s 0, 0) «перепрыгнет» на близкую фазовую траекторию и уйдет по ней сколь угодно далеко. В реальной системе (скажем, шайба на льду) этому помешает трение, но при очень малом трении шайба все равно улетит далеко, а при достаточном заметном трении нужно уже рисовать другой фазовый портрет, так как фазовые траектории не будут прямыми, параллельными оси Os (подумайте, как они могут выглядеть).