Александр Филиппов - Многоликий солитон

Итак, совсем простые средства позволяют довольно много узнать о свойствах очень непростой системы. Здесь, однако, уместно сделать предостережение. То, что маятник непростой прибор, по-видимому, ясно. Недаром он послужил Галилею, Гюйгенсу и Ньютону одним из основных инструментов, с помощью которых они открыли законы механики. Хорошо послужит он и в наших попытках разобраться с нелинейными явлениями.

А вот простота принципа подобия и соображений размерностей несколько обманчива. Это довольно «сильный» принцип, но его применение требует очень хорошего понимания физической сущности явления, к изучению которого он применяется, а общих правил как достичь такого понимания — нет *). Применение принципа подобия в более сложных задачах — это в какой-то мере искусство. Потому-то так долго и не понимали это открытие Ньютона, а когда поняли, то начались бесконечные споры о его смысле, возможностях применения в тех или иных задачах и даже о его полезности. Эти споры не вполне затихли и сегодня. До сих пор современно звучат слова, сказанные 70 лет назад большим знатоком и пропагандистом анализа размерностей Рэлеем: «Меня часто удивляет, что даже весьма крупные ученые уделяют столь незначительное внимание великому принципу подобия. Нередко случается, что результаты кропотливых исследований преподносятся как новые «законы», которые на самом деле можно было бы получить в течение нескольких минут». К сожалению, мы не сможем уделить этому принципу достаточно внимания и рекомендуем читателю самостоятельно тренироваться в открытии с его помощью простых физических законов.

*) Подумайте, почему в живой природе нет подобия. Может ли существовать в точности подобный человеку великан, все размеры которого в 10 раз больше размеров среднего человека!

В качестве упражнения найдите методом размерностей ускорение точки, движущейся равномерно по окружности, и определите период малых колебаний тяжелой невязкой жидкости (например, ртути) в U-образной трубке. Некоторые другие примеры встретятся позже, а сейчас настало время вспомнить еще более великий принцип.

Кинетическая энергия грузика, подвешенного на нити и совершающего малые колебания, равна 1/2 mv 2= 1/2 ml 2(φ') 2, а потенциальную энергию легко найти с помощью рис. 4.5.

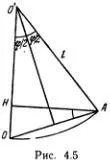
Так как ( ОА ) = 2 l sin(φ/2), то ( ОН ) = 2 l sin 2(φ/2), и потенциальная энергия равна 2mgl sin 2(φ/2). Полная энергия Е = 1/2 ml 2(φ') + 2mgl sin 2(φ/2).

Удобно намного преобразовать это соотношение, сделав все его члены безразмерными:

(φ') 2/ω 0 2+ 4 sin 2(φ/2) = 2Е/ m ω 0 2 l 2. (4.3)

В правой части здесь написано отношение полной энергии маятника к кинетической энергии точки с массой m , равномерно вращающейся по окружности радиуса l с периодом . Обозначим эту энергию буквой Е 0, так что правая часть равна отношению Е/Е 0. Если амплитуда качаний φ Mмала, то sin(φ/2) 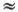φ/2, и закон сохранения энергии (4.3) имеет совсем простой вид

(φ') 2/ω 0 2+ φ 2 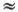Е/Е 0, Е 0= 1/2 m ω 0 2 l 2. (4.4)

Полную энергию удобно выразить через амплитуду φ M. В крайней точке, где φ = φ M, угловая скорость равна нулю. Из уравнения (4.3) поэтому следует, что

Е/Е 0= 4 sin 2(φ M/2) 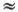φ M 2,

где приближенное равенство, как всегда, относится к малым колебаниям.

С законом сохранения энергии связаны два новых способа наглядного графического изображения движений и других механических систем. Обычный способ — это изображение зависимости φ( t ). Например, график простого гармонического колебания φ = φ Msin(ω 0t) позволяет наглядно представить положение грузика в разные моменты времени (рис. 4.6).

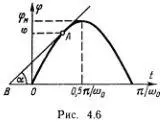
С помощью этого графика можно также найти скорость грузика в любой заданный момент. Она определяется углом наклона касательной BА к кривой в точке А с координатами ( t , φ( t )), т. е. φ' = tg α. На графике, однако, не видно, как распределяется полная энергия при движении и как она связана с амплитудой. Для наглядного представления изменения кинетической и потенциальной энергий грузика нарисуем энергетическую диаграмму.

Нарисуем зависимость потенциальной энергии грузика U (φ) от его положения. В формуле (4.4) потенциальную энергию представляет слагаемое φ 2, а кинетическую Т — слагаемое (φ') 2/ω 0 2. На графике удобнее откладывать отношения U/Е 0, Т/Е 0, Е/Е 0.

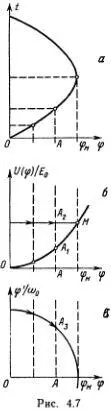
Отложим по горизонтальной оси отрезок ОА , длина которого равна φ( t ), а в направлении вертикальной оси отложим отрезок ( АА 2) = Е/Е 0, причем ( АА 1) = U/Е 0, ( А 1 А 2) = Т/Е 0(рис. 4.7, б). Так как полная энергия постоянна, то точка А 2при изменении t будет двигаться по прямолинейному отрезку А 2 М , а точка А' — по параболе ( U (φ) /Е 0) = φ 2. На энергетической диаграмме видно, как перераспределяется полная энергия между кинетической и потенциальной составляющими при различных значениях φ и как амплитуда связана с полной энергией. Если нарисовать над энергетической диаграммой график φ( t ) (рис. 4.7, α), то можно наглядно увидеть зависимость кинетической и потенциальной энергии от времени. Когда маятник движется из нижнего положения к крайнему правому, где φ = φ M, изображающая точка А 2движется направо до точки М, а затем возвращается налево. Как при этом меняются кинетическая и потенциальная энергия, видно достаточно ясно, но скорость определять не очень удобно (нужно вычислять квадратный корень из длины отрезка А 1А 2). Чтобы следить также и за положением и скоростью грузика, удобно представить движение еще одним способом.

Нарисуем под нашими двумя диаграммами еще одну, на которой по оси абсцисс по-прежнему будем откладывать значения φ, а по оси ординат отложим значения φ'/ω 0в тот же момент времени (рис. 4.7, в). Тогда при движении грузика точка А 3будет описывать окружность с радиусом, равным φ M= 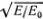. Это видно из уравнения (4.4), так как (ОА) = φ( t ) и (АА 3) = φ'( t )/ω 0. В случае простого гармонического колебания (ОА) = φ Msin(ω 0t), (АА 3) = φ Mcos(ω 0 t ), и ясно, что точка А 3вращается по окружности равномерно.