Александр Филиппов - Многоликий солитон
- Название:Многоликий солитон
- Автор:
- Жанр:
- Издательство:Наука, гл. ред. физ.-мат. лит.
- Год:1990
- Город:Москва
- ISBN:5-02-014405-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Филиппов - Многоликий солитон краткое содержание
Одно из наиболее удивительных и красивых волновых явлений — образование уединенных волн, или солитонов, распространяющихся в виде импульсов неизменной формы и во многом подобных частицам. К солитонным явлениям относятся, например, волны цунами, нервные импульсы и др.
В новом издании (1-е изд. — 1985 г.) материал книги существенно переработан с учетом новейших достижений.
Для школьников старших классов, студентов, преподавателей.
Многоликий солитон - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Малые колебания маятника
Чтобы подступиться к решению нелегкой задачи о движениях маятника, рассмотрим сначала малые колебания, когда угол настолько мал, что можно положить sin φ  φ. Уравнение теперь становится линейным (это и есть линеаризация!):
φ. Уравнение теперь становится линейным (это и есть линеаризация!):

, и можно угадать (или вспомнить!) его решение φ = φ M (ω 0 t ) *), которое равно нулю при t = 0. Благодаря линейности уравнения максимальное значение угла φ M формально может быть произвольным числом, но мы, конечно, должны помнить, что при больших значениях φ M наше приближение не годится. Поэтому число φ M должно быть таким, что sin φ M  φ M .
φ M .
*) для этого достаточно вспомнить правило дифференцирования тригонометрических функций. Ниже это движение будет построено другим, геометрическим способом.
Этим решением, разумеется, не исчерпывается все множество решений. Мы заранее предположили, что φ(0) = 0, и этим отбросили, например, решение φ = cos (ω 0 t ), которое тоже легко угадать. Пользуясь линейностью, теперь можно найти и общее решение, складывая sin (ω 0 t ) и cos (ω 0 t ), умноженные на произвольные амплитуды. Ясно, что этим способом получается любое колебание, так как первое решение позволяет получить любое значение скорости в начальный момент, а второе — задать любое начальное положение.
Самое общее малое колебание можно получить и другим способом, понимание которого очень полезно. Заметим, что движение φ = φ M sin(ω 0 t ) можно наблюдать, пустив другие часы отсчитывать время в момент t 0 (по старым часам). При новом отсчете времени то же самое движение будет выглядеть как φ = φ M sin[ω 0 (t + t 0 ) ].
Нетрудно проверить, что это решение при любых t 0 удовлетворяет уравнению 4.1. Отсюда следует, что если движение φ = φ M sin(ω 0 t ) возможно, то и движение φ = φ M sin[ω 0 (t + t 0 ) ] также возможно. А это движение уже самое общее, поскольку подбором φ M и t 0можно задать любые начальные значения скорости и положения.
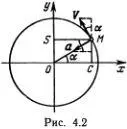
Решение уравнения для малых колебаний можно найти совсем простым способом. Достаточно вспомнить геометрическое определение тригонометрических функций и закон движения материальной точки по окружности. Пусть точка М движется по окружности единичного радиуса с постоянной скоростью V = ω 0(рис. 4.2). Скорость V направлена по касательной, и ее проекция на ось Оу равна ω 0cos α , где α = ω 0 t (радиан). Точка S совершает гармоническое движение, длина отрезка ( OS ) = sin ω 0 t , и ее скорость v равна проекции скорости V на ось Оу , т. е. v = ω 0cos(ω 0 t) . Полное ускорение α направлено к центру и равно 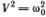 (радиус окружности равен 1). Ускорение точки S равно проекции ускорения а на ось Оу , т. е.
(радиус окружности равен 1). Ускорение точки S равно проекции ускорения а на ось Оу , т. е.  . Таким образом, ускорение точки S равно
. Таким образом, ускорение точки S равно 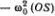 . Если взять ( OS ) = φ, получим φ" =
. Если взять ( OS ) = φ, получим φ" = 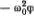 . Обозначив
. Обозначив  , находим, что φ = sin(ω 0 t ) есть решение линейного уравнения для малых колебаний маятника. Заодно вспомним, что период колебаний Т совпадает с временем полного оборота точки М по окружности, т. е. равен
, находим, что φ = sin(ω 0 t ) есть решение линейного уравнения для малых колебаний маятника. Заодно вспомним, что период колебаний Т совпадает с временем полного оборота точки М по окружности, т. е. равен 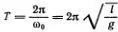 .
.
Маятник Галилея
Эта формула, хорошо известная из школьного курса физики, была впервые найдена Гюйгенсом *). С точностью до числового множителя она, по-видимому, была известна уже Галилею. История ее открытия интересно и подробно описана в упоминавшейся в книге С. Г. Гиндикина, но с одним утверждением, сделанным в ней, можно поспорить. Там сказано (с. 39): «Галилей обнаруживает связь между длиной маятника и частотой его колебаний: квадраты периодов колебаний относятся как длины. Вивиани пишет, что Галилей получил этот результат, «руководствуясь геометрией и своей новой наукой о движении», но никто не знает, каким мог быть теоретический вывод. Быть может, все же Галилей подметил закономерность экспериментально?» Принять это предположение было бы несправедливостью по отношению к Галилею. На опыте он лишь подметил зависимость периода от длины, но закон пропорциональности периода квадратному корню из длины нашел с помощью довольно остроумных рассуждений, которые представляют не только исторический интерес.
*) Гюйгенс получил ее другим способом, основанным на открытом им свойстве изохронности колебаний циклоидального маятника, а рассуждения, приведенные выше, использовал для определения ускорения точки, движущейся по окружности (о циклоидальном маятнике см. в книге: Гиндикин С. Г. Рассказы о физиках и математиках. — 2-e изд. — М.: Наука, 1984. Библиотечка «Квант», вып. 14).
Основным для Галилея был найденный опытным путем закон равной продолжительности качаний маятников одинаковой длины, или изохронизм их колебаний (от греч. «изос» — равный, «хронос» — время). Для дальнейших рассуждений он использовал открытый им закон свободного падения и связь движения по наклонной плоскости со свободным падением. Если слегка модернизировать рассуждения Галилея, как это сделал Л. И. Мандельштам в своих замечательных «Лекциях по колебаниям», прочитанных в 1930 г., то можно даже получить формулу, похожую на формулу Гюйгенса.
Заменим движение грузика по дуге АО из состояния покоя свободным движением по хорде АО (рис. 4.3). Тогда время t, затраченное на это падение, равно времени свободного падения из О" в О . Это следует из известного Галилею факта, что ускорение движения по катету прямоугольного треугольника относится к g, как длина ОА относится к длине ( OO" ) = 2 l (сообразите, почему). Так как 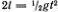 , то четверть периода колебаний равна
, то четверть периода колебаний равна 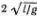 , а полный период
, а полный период  . Галилей рассуждал несколько иначе и ограничился утверждением о пропорциональности времен скатывания по хорде АО и движения маятника по дуге ОА времени свободного падения по вертикали О"О , откуда он и вывел пропорциональность этого времени квадратному корню из длины маятника.
. Галилей рассуждал несколько иначе и ограничился утверждением о пропорциональности времен скатывания по хорде АО и движения маятника по дуге ОА времени свободного падения по вертикали О"О , откуда он и вывел пропорциональность этого времени квадратному корню из длины маятника.
Подлинное рассуждение Галилея легко понять из рис. 4.4. Время скатывания грузика по наклонной плоскости ОА 1А 2 пропорционально квадратному корню из длины (( OA 1 ) для первого маятника и ( ОА 2 ) для второго). Эти длины ОА 1 и ОА 2 пропорциональны длинам маятников ( O 1O ) = l 1и ( O 2O ) = l 2 . С учетом закона свободного падения отсюда следует, что Т пропорционально  для подобных колебаний (т. е. с одинаковым максимальным углом отклонения φ).
для подобных колебаний (т. е. с одинаковым максимальным углом отклонения φ).
Интервал:
Закладка:










