Александр Филиппов - Многоликий солитон

Используя изохронность, доказываем, что это верно для любых колебаний.

Для малых колебаний рассуждения Галилея совершенно правильны. Малые колебания действительно изохронны. Как мы теперь понимаем, изохронность прямо следует из линейности . Действительно, если колебание с единичной амплитудой определяется функцией φ = sin (ω 0 t ), то колебание с амплитудой φ M , в силу линейности, можно найти простым умножением на φ M . Это и значит, что период остается неизменным. Остальная часть рассуждения Галилея особенно интересна тем, что в ней содержится намек на использование соображений о подобном поведении подобных систем. В ясном виде принцип подобия впервые сформулировали Ньютон и Гук. Это настолько полезная вещь, что стоит сделать небольшое отступление.

Принцип подобия Ньютона—Гука оставался в забвении более ста лет, пока его не возродил Фурье в упоминавшейся выше работе «Аналитическая теория теплоты». Он ввел очень важные понятия размерности физической величины и принцип однородности по размерностям . Измерение всех механических величин сводится к измерению нескольких основных, в качестве которых обычно берут длину (размерность L ), время (размерность Т ) и массу (размерность М ). Остальные величины назовем « производными ».

Так, измерение площади сводится к измерению длин. Чтобы измерить площадь прямоугольника S , мы измеряем длины его сторон и перемножаем их. Если обе стороны умножить на одно и то же число с , то площадь умножится на с 2. Это означает, что размерность площади равна квадрату размерности длины, и этот факт можно записать с помощью « формулы размерности » [ S ] = L 2. Формула размерности для S говорит нам, что площади любых фигур умножаются на одно число с 2, если все линейные размеры умножить на с (например, при фотоувеличении). Если бы мы не знали, как вычислить площадь круга радиуса R , то из формулы размерности получили бы, что S = cR 2, где c — некоторое число, о котором формула размерности ничего не говорит. Измерив c для какого-нибудь круга, мы с помощью формулы размерности будем знать, как вычислить площадь любого круга.

Точно так же, исходя из определения скорости равномерного движения v = ( x 2- x 1)/( t 2- t 1), можно написать для нее формулу размерности [ v ] = LT -1. Она просто означает, что при увеличении всех расстояний в c Lраз и всех промежутков времени в c Траз скорость умножится на число c L/c T. Обычно когда записываются формулы для физических величин, они всегда сопровождаются указанием на единицы измерения ( S [см 2], v [см • с -1] и т. д.). Это указание одновременно дает нам и размерность величины. Так как ускорение измеряется, скажем, в см • c -2, то формула размерности для ускорения есть, очевидно, [α] = LT -2.

Аналогично легко найти формулы размерности для силы [F] = MLT -2, для энергии [Е] = ML 2T -2и для других производных величин. Показатели степеней в формулах размерности называются показателями размерности. С ними можно обращаться, как с обычными показателями степени.

Например, возьмем формулу «сила = масса × ускорение». Если увеличить все линейные размеры в c Lраз, промежутки времени в c Tраз и массы в с Mраз, то ускорение увеличится в c L/c 2 Tраз, а сила в с Mc L/c 2 Tраз. Это мы и запишем с помощью формулы для силы. Очевидно, что ее можно получить и так: [F] = М [а] = MLT -2, т. е. с формулами размерности можно обращаться, как с обычными формулами.

Принцип однородности по размерностям требует чтобы обе части равенства, выражающего физический закон, имели одинаковые формулы размерности . Это правило хорошо известно и используется для проверки правильности полученных при вычислениях соотношений. Если мы, например, вычисляли объем какой-то сложной фигуры и получили для него выражение, измеряемое в квадратных сантиметрах (размерность L 2), то нужно искать ошибку в вычислениях. Особенно интересно, однако, обратное применение этого принципа для получения самих формул.

Получим, например, закон Галилея для свободного падения тела. Пройденный за время падения t путь s может зависеть еще от массы тела m и от действующей на него силы mg. Мы можем предположить поэтому, что s = kt dm b(mg) с, где d, b, с, k — некоторые числа. Формула размерности для правой части есть T dM b+c[α с] = M b+cT d-2cL с. Формула размерности для левой части [s] = L. Приравнивая показатели размерности, находим с = 1, d - 2с = 0, b + с = 0, т. е. d = 2, b = -1, так что s = kgt 2, где k — неизвестное число. Его уже нельзя определить из соображений подобия и размерности.

Найдем формулу Гюйгенса для линейных колебаний маятника. Период Т может зависеть от длины l , массы грузика m и действующей на грузик силы f , т. е. Т = dm af bl c . Отсюда находим уравнение размерностей [ Т ] = M α +b L b+cT -2b, т. е. а + b = 0, b + с = 0, -2b = 1. для периодов колебаний получаем формулу

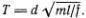
При f = mg получается формула Гюйгенса, но с неизвестным множителем d .

Интересно, что этим способом мы получили более общую формулу для периода колебаний, которая годится не только для маятника в поле силы тяжести. Например, если грузик имеет электрический заряд q и помещен в однородное и постоянное электрическое поле Е между обкладками конденсатора, то на него действует сила f = mg + qE . Зная формулу Гюйгенса, мы определяем d и для маятника в электрическом поле сразу находим период колебаний

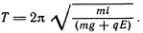
Конечно, таким простым способом можно получить полный ответ далеко не всегда. Рассмотрим нелинейные колебания маятника в поле силы тяжести. Теперь зависимостью периода от амплитуды, как мы сделали это выше, пренебречь нельзя. Небольшое размышление показывает, что наши рассуждения остаются верными, но d нельзя считать просто числом — d оказывается функцией безразмерного выражения, зависящего от амплитуды колебания, например, от отношения длины дуги s M= l φ Mк длине маятника l . Таким образом, для периода произвольных колебаний получаем

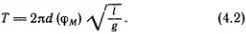
Так как при малых значениях φ Mдолжно быть d 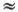1, то функция d (φ M) удовлетворяет условию d (φ M) → 1 при φ M→ 0.

Легко сообразить, что d (φ M) 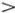1. Действительно, [sin φ] 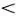[φ] и возвращающая сила для нелинейного маятника всегда меньше, чем для линейного маятника. Нелинейная сила дает меньшее ускорение грузику на всем пути, а значит, период нелинейного колебания всегда больше периода линейного колебания. Это отличие возрастает с ростом амплитуды φ M. Можно доказать, что d (φ M) возрастает с ростом φ M и что период неограниченно возрастает, если φ M→ π.