Александр Филиппов - Многоликий солитон

*) Как мы уже говорили, «досадным» исключением оставалась лишь гидродинамика.

Почему линейность так упрощает решение задачи? Проще всего это понять на простых примерах. Рассмотрим уравнение ах + y = 0, решения которого — это пары чисел (x, у), при подстановке которых оно обращается в тождество. Ясно, что всякое решение можно записать в виде (х 0, -ax 0), где x 0— произвольное число. Если изобразить решения точками на плоскости, то все решения лежат на прямой ОА, проходящей через точки О = (0, 0) и А = (1, -a). Если мы знаем только одно решение А, то, пользуясь линейностью, можно получить все решения умножением на произвольное число: х 0А = (х 0, -aх 0). Математик скажет, что совокупность всех решений этого уравнения образует линейное одномерное многообразие . Для определения всех его точек достаточно задать одну точку, отличную от О (0, 0), например, А = (1, -a). Если — две точки этого многообразия, то точка А 3= c 1A 1+ с 2А 2= 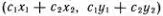, при любых с 1и с 2тоже принадлежит этому многообразию (т. е. точка А 3тоже лежит на прямой ОА).

Точно также можно найти все решения уравнения ах + by + z = 0, т. е. тройки чисел (x, y, z), при подстановке которых уравнение обращается в тождество. Можно убедиться, что достаточно знать два решения, например, 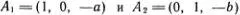, а все остальные получаются их линейными комбинациями , т. е. 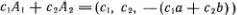. Это пример двумерного линейного многообразия . Геометрически можно изобразить его как плоскость в трехмерном пространстве (попробуйте проверить эти утверждения и нарисовать такую плоскость).

Рассмотрим теперь более близкий к физике пример колебаний грузика на пружине. Отклонение грузика от положения равновесия x(t) подчиняется уравнению Ньютона 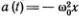, где а(t) — ускорение грузика в момент t , ω 0— круговая частота, ω 0 = 2π/ Т , а Т — период колебаний грузика. Если x 1(t) и x 2(t) — два решения этого уравнения, описывающие какие-то два движения, то и любая их линейная комбинация — тоже решение (т. е. х 3(t) — возможное движение) *). Совокупность всех решений также образует линейное многообразие.

*) Так как ускорение a(t) линейно зависит от x(t) .

Рассмотрим два движения: x 1(t) = cos(ω 0 t ) и x 2(t) = sin(ω 0 t ). Взяв , можно написать произвольную линейную комбинацию из x 1 и x 2 : 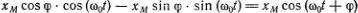. Так получается самое общее выражение для отклонений грузика при колебаниях с амплитудой х M и фазой φ. По аналогии с рассмотренными нами алгебраическими уравнениями можно сказать, что линейное многообразие возможных колебаний двумерно. Каждое колебание грузика можно представить точкой на плоскости ( с 1, с 2 ), и эти точки также образуют линейное многообразие.

Над этими простыми примерами стоит как следует подумать. Важно понять, во-первых, что любое колебание грузика можно представить в виде суммы двух линейно независимых, т. е. не выражающихся друг через друга в виде линейных комбинаций колебаний x 1 = cos(ω 0 t ) и x 2 = sin(ω 0 t ) (вместо этих можно взять и другие линейно независимые решения). Наоборот, пусть известны два возможных колебания x 1(t) и x 2(t) , отношение которых не постоянно, — такие колебания будут линейно независимыми . Тогда любое другое движение можно получить, подобрав подходящие числа с 1 и с 2 и складывая колебание с 1x 1(t) с с 2x 2(t) . Важно, что при этом не нужно знать даже само уравнение. Достаточно иметь два независимых колебания и знать, что выполнен принцип линейности или принцип сложения колебаний.

Если линейности нет, то все выглядит гораздо сложнее. Возьмем самое простое уравнение y 2+ аx 2= 0. Сразу ясно, что многообразие решений (x, у) будет иметь совершенно разный вид при разных знаках а . При а 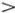0 оно состоит из единственной точки О = (0, 0). При а = 0 — это точки, лежащие на оси Оx , т. е. точки ( x 0 , 0), где x 0 — любое число. Если же а 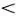0, то все решения имеют вид 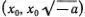или , или , т. е. лежат либо на прямой ОА , либо на прямой ОB (рис. 3.9).

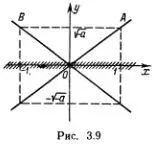
Ясно, что в этом случае многообразие решений нелинейно. Например, сумма двух написанных решений с одним и тем же х 0 равна (2 х 0 , 0), а х = 2 х 0 , у = 0 не удовлетворяет нашему уравнению при .

Так обстоит дело в самом простом случае. При усложнении уравнения уже совсем не просто выяснить, имеет ли оно решения, и если имеет, то сколько и как эти решения зависят от параметров, входящих в уравнения. В нашей простой задаче единственный параметр — это число а . При а 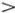0 есть только нулевое решение, при а = 0 решения образуют линейное многообразие, а при а 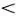0 многообразие решений становится нелинейным. В этом примере нелинейное многообразие устроено слишком просто, но небольшое изменение уравнения (скажем, добавка к левой части слагаемого bх , где число b может быть очень малым) приводит к очень серьезным, качественным изменениям структуры множества решений (убедитесь в этом!).

Вообще, такая сильная, качественная зависимость решений от параметров, появление новых решений (или их исчезновение) — самое характерное свойство нелинейных уравнений. С простыми примерами такого проявления нелинейности в движениях тел мы сталкиваемся очень часто. Когда мы пытаемся сдвинуть с места стоящий на ровном месте автомобиль, мы постепенно увеличиваем усилие, но автомобиль не двигается, пока усилие не достигнет определенного значения. После того как автомобиль начнет двигаться, его довольно легко разогнать, прилагая меньшее усилие. Этот эффект возникает из-за нелинейности силы трения — при движении автомобиля сила трения меньше, чем в покое. Нелинейность этого типа можно назвать «пороговой» нелинейностью. При достаточно малых воздействиях (ниже «порога») система находится в одном состоянии (автомобиль не движется), при достижении порога система переходит в другое состояние, в котором воздействие можно уменьшить или даже убрать (катящийся автомобиль может двигаться некоторое время по инерции).