Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

В законе Ньютона обращают на себя внимание по меньшей мере три поразительных факта.

Бросается в глаза удивительная аналогия характера гравитационных сил с взаимодействием совершенно другой природы — электрических зарядов (закона Кулона).

F = ±[e 1] · [e 2]/ r 2.

Мы не будем касаться причин этого любопытного совпадения и ограничимся констатацией факта. Правда, с другой стороны, есть и кардинальное отличие: гравитационные «заряды» имеют всегда только один знак.

Закон Ньютона предполагает, и на этом мы задержимся дольше, что тяготение распространяется с бесконечно большой скоростью.

Действительно, закон тяготения подразумевает, что для определения силы притяжения в каждый данный момент времени достаточно знать расстояние между телами в тот же самый момент времени. Как изменяется расстояние со временем, совершенно не существенно, — говоря учено, несущественна пространственно-временная биография взаимодействующих тел.

Посмотрим, что изменилось бы в законе Ньютона, если бы скорость тяготения была конечна, а во всем остальном закон взаимодействия остался бы прежним.

Допустим, два тела взаимодействуют по закону Ньютона. При этом тяготение распространяется с конечной скоростью с . Если тела покоятся — все остается по-старому. Но не то, если они движутся друг относительно друга.

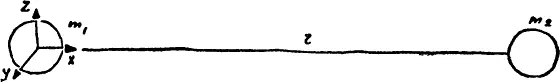
Конечно, в первую очередь возникает вопрос, что означает: скорость распространения тяготения конечна и равна с ? В какой системе отсчета? Поэтому примем условно некую «абсолютную систему», в которой скорость тяготения и есть с.

Мы не знаем и не хотим знать, почему скорость распространения тяготения конечна: может быть, потому, что тела постоянно посылают волны тяготения, которые распространяются в пространстве с конечной скоростью, может быть, по другой причине. Мы хотим просто установить, как изменится при этом закон Ньютона.

Для простоты рассмотрим только тот случай, когда первое тело покоится в нашей «абсолютной системе отсчета». Пусть в момент времени t 0 = 0, который мы выберем за начало отсчета, второе тело начинает равномерно приближаться к первому со скоростью V . Когда тела покоились, сила взаимодействия определялась законом Ньютона:

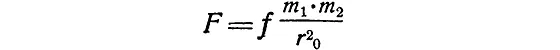
где r 0— расстояние между покоящимися телами. В какой-то момент времени t расстояние между телами оказалось равным r ( t ) = r 0 – Vt .

А чему равна сила взаимодействия? Так как скорость распространения тяготения конечна, взаимодействие между телами будет определяться расстоянием не в данный момент времени, а в какой-то более ранний. «Волна» тяготения, которая добралась в момент t до первого тела, была послана вторым в какой-то более ранний момент ( t 1 < t ).

Этот момент легко определяется, но, возможно, не стоит так углубляться в формулы. Тем более что мы умалчиваем о более существенном.

Действительно, мы, по сути дела, отмахнулись от ответа, в какой системе определена скорость тяготения, а пока нет системы отсчета, всякие разговоры о скорости распространения тяготения абсолютно бессодержательны.

Естественно, такая абсолютная система отсчета (если она существует) должна быть связана не с двумя наугад взятыми телами (как в нашем примере), а как-то со свойствами самого пространства (может быть, с системой неподвижных звезд?).

Сразу возникает мысль: а нельзя ли, исследуя тяготение, реально отыскать абсолютную систему? А как, между прочим, найти скорость распространения тяготения в других системах отсчета?

В общем стоит допустить, что скорость распространения силы тяготения конечна, и физическая картина основательно запутывается, не говоря уже о том, что уравнения движения небесных тел весьма усложняются.

Ньютон сразу отбросил все подобные трудности. Он положил, что скорость распространения тяготения бесконечна. И тем самым ввел дальнодействие.

Но честно признаемся, эту идею можно принять лишь с некоторым усилием. Против нее протестует наше чувство. Все известные процессы распространяются с конечной скоростью. Даже свет! А тяготение почему-то такое странное исключение.

В общем можно только лишний раз поразиться гению и интуиции Ньютона.

Забегая вперед, заметим: теперь, после Эйнштейна, мы знаем, что Ньютон ошибся. Скорость распространения поля тяготения конечна и равна 300 000 километров в секунду. Кроме того, эта скорость обладает странным качеством — она постоянна в любой системе отсчета и не изменяется при переходе от одной системы к другой.

Ввиду колоссального значения скорости распространения тяготения поправки к закону Ньютона, обусловленные «запаздыванием», настолько ничтожны, что не удивительна двухвековая уверенность в безукоризненной справедливости закона тяготения.

Покончим на этом с «удивлением № 2» и перейдем к следующему.

Наиболее поразительно в законе Ньютона, без сомнения, то, что сила тяготения полностью определяется инертными массами тел.

Сила тяготения совершенно не зависит от химического состава тел, от электрических зарядов, которые несут тела, от агрегатного состояния.

Тяготение определяется только массой, то есть в конечном счете инерцией тяготеющих тел.

Интуитивно чувствуется, что, очевидно, между инерцией и тяготением существует какая-то глубокая связь.

Однако тяготение и инерция, казалось бы, настолько различные физические свойства, что физики неоднократно экспериментально проверяли, действительно ли масса, определяемая законами механики (инертная масса), и масса в законе всемирного тяготения — это одно и то же.

Первым снова был Галилей.

Тот факт, что все тела в поле земного тяготения падают с одинаковым ускорением, — главное доказательство равенства инертной и тяжелой массы.

Убедимся в этом. В поле Земли на тело массы m действует сила

F = f · m т · M т/ r 2.

Здесь m т— тяжелая масса тела, определяемая из закона тяготения; M т— тяжелая масса Земли; r — расстояние до центра Земли [30] .

Не будем предрешать равенство тяжелой и инертной массы и, используя второй закон механики, найдем ускорение тела в поле земного тяготения:

f · (m т · M т)/( m и · r 2) = g,

где m и— инертная масса тела; g — ускорение в поле тяготения Земли.

В этой формуле сомножитель f · M т/ r 2для всех тел на поверхности Земли постоянен; второй сомножитель — отношение m т/ m икак мы допустили, — может меняться в зависимости от природы и характера физических тел.