Volodymyr Bezverkhniy - Review. Benzene on the basis of the three-electron bond. Theory of three-electron bond in the four works with brief comments (review). 2016.

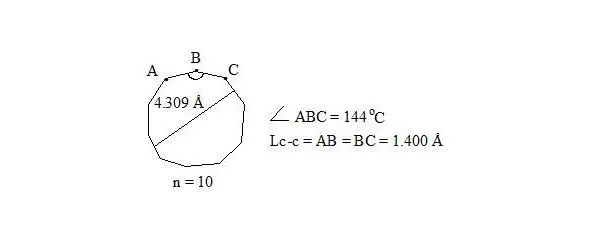
cyclodecapentaene, distance

Whereas central electrons of three-electron bonds have opposite spins, then interaction through the cycle is possible. But distances between central electrons on opposite sides, which interact through the cycle, are extremely long (4.309 Å if accept Lс-с = 1.400 Å for regular decagon), angular pressure is high (24°) and that’s why stabilization at the expense of interaction through the cycle at such long distance will be low and cannot cover energy consumption for creation of planar molecule.

Cyclodecapentaene was received in the form of crystalline substance at – 80°С. On spectrums ¹³С-NMR and ¹Н-NMR it was determined, that compound is non-planar and is olefin, that is logical on the basis of long distance between central electrons [8, p. 84], [12].

Lets draw our attention to the fact that in going from benzene to cyclooctatetraene and to cyclodecapentaene distance increases not only between central electrons on the opposite sides (interaction through the cycle), but also between neighboring central electrons.

Lets show it on figure.

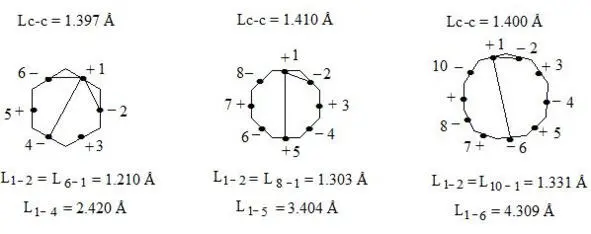
benzene on the basis of the three-electron bond, distance between electrons (benzene, cyclooctatetraene, cyclodecapentaene)

As we can see distance between neighboring central electrons 1 and 2 in benzene makes up 1.210 Å, in regular octagon 1.303 Å, and in regular decagon 1.331 Å (almost as distance between carbon atoms in ethene molecule). That is by going from benzene to regular octagon and decagon not only angular pressure (0°, 15°, 24°) and distance between central electrons increase, which are situated on the opposite sides (2.420 Å; 3.404 Å; 4.309 Å), as well as distance between neighboring central electrons 1 and 2 (1.210 Å; 1.303 Å; 1.331 Å), that causes considerable weakening of interaction through the cycle in regular decagon. That’s why regular hexagon (benzene) is ideal aromatic system. As angular pressure is equal to zero, distances between central electrons both neighboring and situated on the opposite sides are minimal (accordingly 1.210 Å and 2.420 Å). I.e. interaction through the cycle will be maximal. By going to regular decagon these advantages will be lost. That’s why cyclodecapentaene is olefin.

Let us note for comparison that if we take Lc-c = 1.400 Å for the planar cyclooctatetraen, we will have L (1—5) = 3.380 Å, L (1—2) = L (8—1) = 1.293 Å which vary just slightly from the above mentioned distances between the central electrons at Lс-с = 1.410 Å.

By means of the interaction through the cycle together with the three-electron bond, aromaticity of coronen, [18] -annulene, naphthalene and other organics substances can be explained (see conclusion).

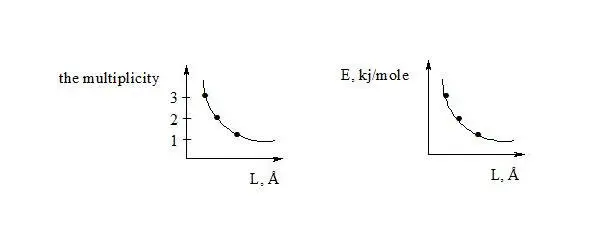
Now let’s pass to the definition of delocalization energy of benzene. It is easy to show, that relation multiplicity = f (L) and Е = f (L), where multiplicity is multiplicity of bond, L – length of bond in Å, Е – energy of bond in kj/mole will be described by function y = a + b/x + c/x² for any types of bond (C-C, C-N, C-O, C-S, N-N, N-O, O-O, C-P).

We shall consider ethane, ethylene and acetylene to be initial points for the c-c bond.

For lengths of bonds let us take the date [7]:

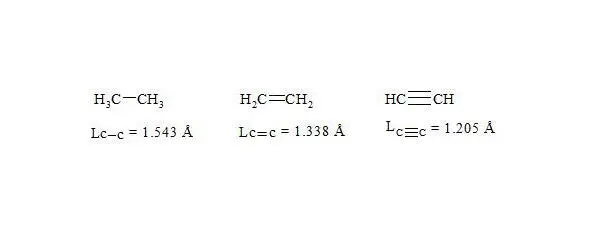
bond lengths in ethane, ethylene and acetylene

As usual, the С-С bond multiplicity in ethane, ethylene and acetylene is taken for 1, 2, 3.

For energies of bonds let us take the date [7, p. 116]:

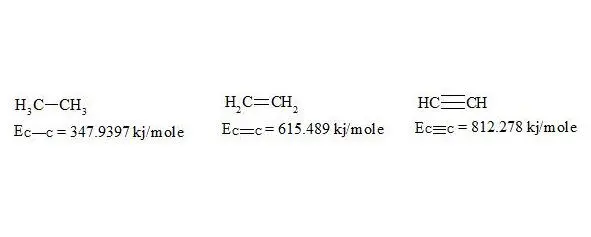
energies of bonds in ethane, ethylene and acetylene

The given bond energies (according to L. Pauling) are bond energy constants expressing the energy that would be spent for an ideal rupture of these bonds without any further rebuilding of the resulting fragments. That is, the above mentioned energies are not bond dissociation energies.

Having performed all necessary calculations we obtain the equation:

(1)

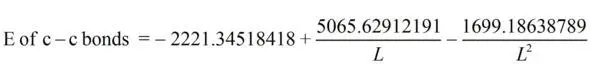
(2)

From these equations we find:

c—c benzene multiplicity (L = 1.397 Å) = 1.658

c—c graphite multiplicity (L = 1.42 Å) = 1.538 ≈ 1.54

Ec—c benzene (L = 1.397 Å) = 534.0723 kj/mole

Ec—c graphite (L = 1.42 Å) = 503.3161 kj/mole

Being aware that the benzene has the three-electron bonds and also the interaction through the cycle, we can calculate the interaction through the cycle energy.

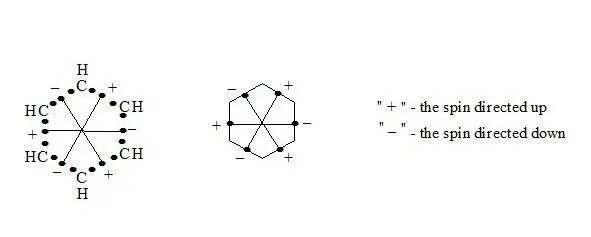
benzene on the basis of the three-electron bond, interaction through the cycle

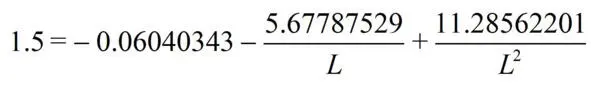
(3)

from the equation we find L = 1.42757236 Å.

So, if the benzene molecule had a «clean» three-electron bond with a 1.5 multiplicity the c-c bond length would be L = 1.42757236 Å.

Now let us determine the energy of the «clean» three-electron bond with a 1.5 multiplicity knowing its length L = 1.42757236 Å:

Ec – c (L =1.42757236 Å) = 493.3097 kj/mole

Taking into account that the benzene c-c bond energy with a 1.658 multiplicity is equal to Ec-c benzene = 534.0723 kj/mole, the difference will make:

ΔE = 534.0723 kj/mole – 493.3097 kj/mole = 40.7626 kj/mole.

40.7626 kj/mole is the energy of interaction through the cycle per one c-c bond. Therefore, the energy of interaction through the cycle will be two times higher:

E 1= 40.7626 kj/mole ∙ 2 = 81.5252 kj/mole (19.472 kcal/mole)

It is clear that the three interactions through the cycle present precisely the working benzene delocalization energy which is:

E = 3E 1= 3 ∙ 81.5252 kj/mole = 244.5756 kj/mole (58.416 kcal/mole)

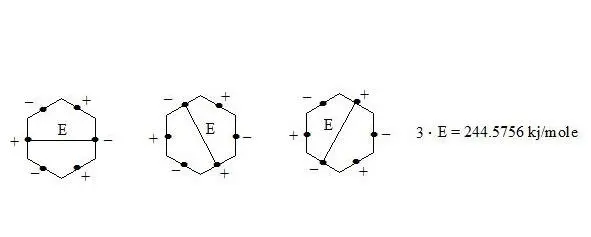
benzene on the basis of the three-electron bond, delocalization energy

It is also possible to calculate the benzene molecule energy gain in comparison with the curved cyclohexatriene (let us assume that energy of C-H bonds in these molecules is similar). For this we calculate the sum of energies of single and double c-c bonds in cyclohexatriene:

E 2= 3Ec—c +3Ec═c = 2890.286 kj/mole

The energy of six benzene c-c bonds with a 1.658 multiplicity is equal to:

E 3= 6 · 534.0723 kj/mole = 3204.434 kj/mole

Therefore, the gain energy of benzene compared to cyclohexatriene will amount to:

E = E 3 – E 2= 3204.434 kj/mole – 2890.286 kj/mole = 314.148 kj/mole (75.033 kcal/mole).

Let’s show more detailed calculation of ratios for our mathematical relations. Let’s consider relation Multiplicity = f (L) and E = f (L) for С-С bonds, where multiplicity is multiplicity of bond, L – length of bond in Å, Е – energy of bond in kj/mole.

As initial points for the given bonds we will use ethane, ethene and acetylene. For the length of bonds let us take the findings [7]:

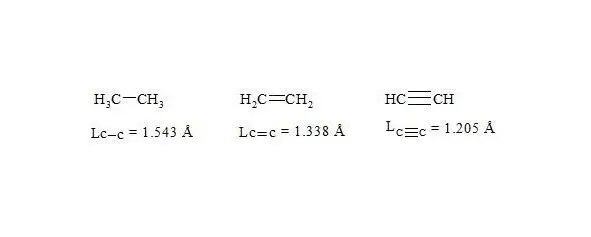
bond lengths in ethane, ethylene and acetylene

As usual, the С-С bond multiplicity in ethane, ethylene and acetylene is taken for 1, 2, 3. For the energy of bonds let us take the findings [7, p. 116]:

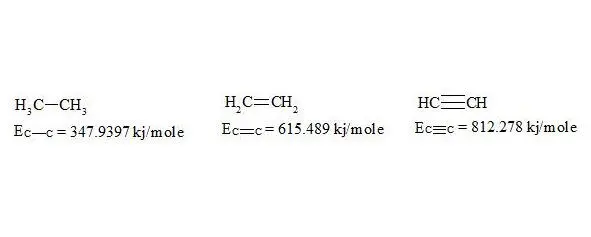
energies of bonds in ethane, ethylene and acetylene

If we have two variants and we received the set of points and we marked them on the plane in the rectangular system of coordinates and if the present points describe the line equation y = ax + b that for choose the coefficients a and b with the least medium-quadratic deflection from the experimental points, it is needed to calculate the coefficients a and b by the formulas:

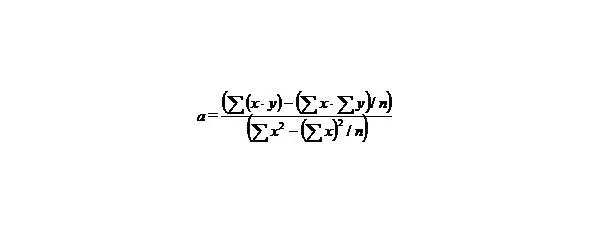
(4)

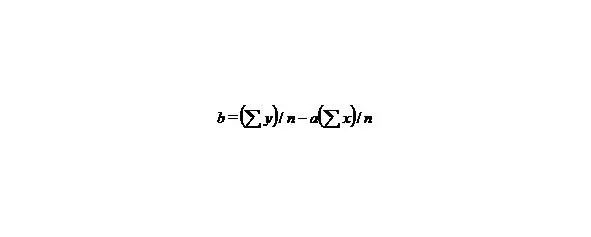
(5)

n-the number of given values x or y.

If we want to know how big is the derivative, it is necessary to state the value of agreement between calculated and evaluated values y characterized by the quantity:

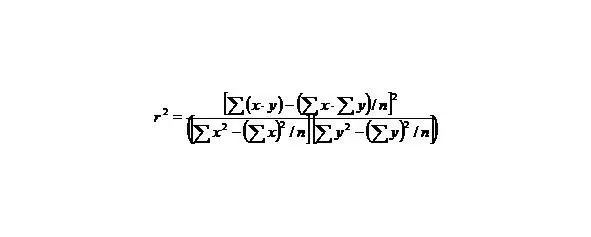
(6)

The proximity of r 2to one means that our linear regression coordinates well with experimental points.

Let us find by the method of selection the function y = a + b/x + c/x 2describing the dependence multiplicity = f (L) and E = f (L) in best way, in general this function describes this dependence for any chemical bonds.

Let us make some transformations for the function y = a + b/x + c/x 2, we accept

X = 1/x,

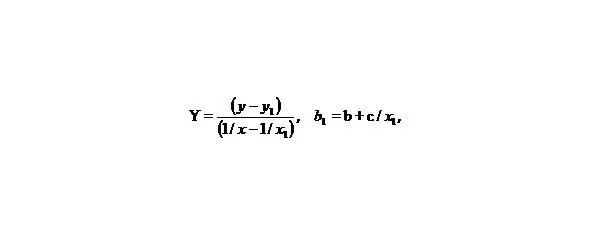
than we’ll receive: Y = b 1+ cX, that is the simple line equality, than

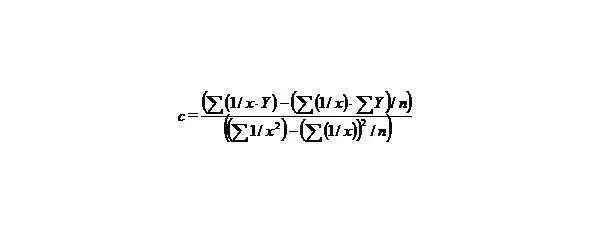
(7)

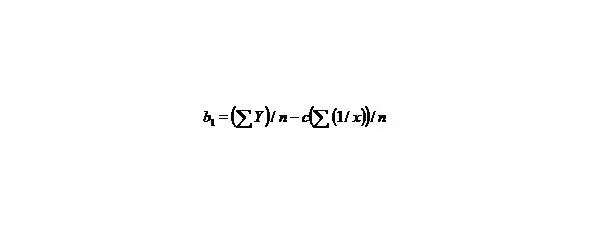
(8)

n—the number of given value Y.

Let us find a from the equality:

∑y = na + b∑ (1/x) + c∑ (1/x 2), (9)

when n = 3.

Let us find now multiplicity = f (L) for C─C, C═C, C≡C.

Table 1. Calculation of ratios for relation Multiplicity = f (L).