Маркус Сотой - Тайны чисел: Математическая одиссея

Возьмите кусок проволоки и согните его в квадрат. Погрузите его в мыльный раствор, выньте и подуйте. Почему у пузыря, который выходит с другой стороны, не будет формы куба? А если проволока согнута в виде треугольника, почему не получается выдуть пирамидальный пузырь? Отчего, какой бы ни была форма рамки, пузырь получается безупречно сферичным? Ответ состоит в том, что природа ленива, а сфера для природы – самая легкая форма. Пузырь стремится приобрести такую форму, которая использует наименьшую энергию, а последняя пропорциональна площади поверхности. В пузыре содержится заданный объем воздуха, который не меняется при преобразованиях формы. А у сферы, содержащей заданное количество воздуха, – наименьшая площадь поверхности. Это делает ее энергетически выгодной, она использует меньше всего энергии.

Промышленники издавна стремились подражать способности природы делать совершенные сферы. Если вы изготавливаете шарикоподшипники или дробь для ружей, получение правильных сфер может быть вопросом жизни и смерти, поскольку небольшое отклонение от сферической формы может привести к поломке машины или разрыву ружья. 1783 год ознаменовался достижением водопроводчика Уильяма Уоттса из Бристоля, который понял, как воспользоваться предрасположенностью природы к сферам.

Когда жидкие капли расплавленного металла падают с верхушки высокой башни, то в своем падении они подобно пузырям приобретают сферическую форму поверхности. Уоттс заинтересовался тем, что будет, если внизу башни поставить чан с водой, – застынут ли капельки с сохранением идеальной формы при попадании в воду. Он решил проверить эту идею в собственном доме в Бристоле. Загвоздка была в том, что требовалась высота более трех этажей, чтобы дать каплям расплавленного свинца достаточное время для приобретения сферической формы.

Тогда Уоттс пристроил к своему дому еще три этажа и проделал в полах отверстия, чтобы свинец падал сквозь все здание. Соседи были слегка шокированы неожиданным появлением башни, хотя владелец и пытался придать ей готический флер, добавив сверху архитектурные украшения, как у замка. Эксперименты Уоттса оказались настолько успешны, что подобные башни стали появляться по всей Англии и Америке. Его башня по отливу дроби продолжала работать до 1968 г.

Рис. 2.01. Умное использование Уильямом Уоттсом свойств природы для производства дроби

Хотя природа и использует сферу столь часто, как мы можем быть уверены, что не существует какой-то более странной формы, которая окажется энергетически более эффективной, чем сфера? Великий греческий математик Архимед первым предположил, что у сферы на самом деле наименьшая площадь поверхности, когда содержащийся внутри объем фиксирован. Чтобы попытаться доказать это, Архимед начал с выведения формул для площади сферы и для объема, содержащегося в ней.

Вычисление объема, ограниченного изогнутой формой, представляло немалый вызов. Но Архимед применил хитрый прием: необходимо рассечь сферу параллельными разрезами на множество тонких слоев и затем приближенно заменить слои дисками. Он знал формулу для объема диска: нужно было умножить площадь круга на толщину диска. Сложив вместе объемы всех этих дисков разного размера, Архимед получил приближение для объема шара.

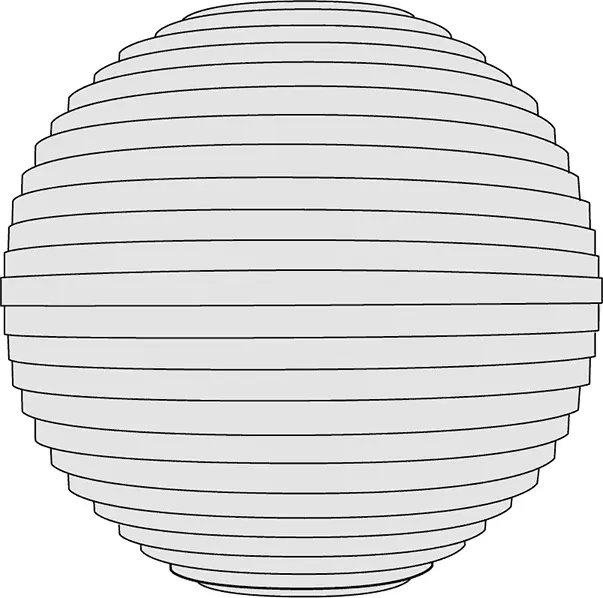
Рис. 2.02. Шар может быть приближен положенными друг на друга дисками разного размера

Затем последовала по-настоящему умная часть. Если он будет делать диски тоньше и тоньше, пока они не станут бесконечно тонкими, то их суммарный объем даст в точности объем шара. Это был один из первых случаев использования идеи бесконечности в математике. Подобная техника стала впоследствии основой математического анализа, развитого Исааком Ньютоном и Готфридом Лейбницем спустя почти две тысячи лет.

Архимед продолжал использовать этот метод для вычисления объемов, ограниченных различными формами. Особенно он был горд открытием того, что объем воздуха в цилиндре, высота которого равна диаметру вписанного в него шара, составляет половину объема шара. Он был так взволнован этим фактом, что завещал, чтобы на его надгробии были высечены цилиндр и шар.

Хотя Архимед нашел успешный метод для вычисления площади сферы и объема ограниченного ею шара, ему не хватило умения для доказательства предположения, что сфера – самая эффективная форма в природе. Поразительно, но лишь к 1884 г. математика была достаточно разработана для того, чтобы немец Герман Шварц сумел доказать, что не имеется таинственных форм, которые могут побить энергетическую эффективность сфер.

Во многих видах спорта используются шары и сферические мячи: теннис, крикет, бильярд, футбол. Хотя природе с легкостью удаются сферы, людям изготавливать их особенно сложно. Это обусловлено тем, что в большинстве случаев мы вырезаем формы из плоских листов материала, которые впоследствии сшиваются либо подвергаются термосклейке. В некоторых состязаниях упор делается на трудности изготовления сфер. Крикетный мяч состоит из четырех кусков формованной кожи, которые сшиваются вместе, поэтому он не вполне сферический. Наличие шва может быть использовано боулерами, подающими мячи, чтобы мяч непредсказуемым образом отскакивал от поля.

В противоположность этому игрокам в настольный теннис необходимы идеально круглые мячи. Мячи изготавливаются склеиванием двух целлулоидных полусфер, но этот метод не слишком-то успешен: более 95 % изделий отбраковываются. Изготовители мячей для пинг-понга немало развлекаются, когда отсортировывают сферы от деформированных мячей. Специальное ружье запускает мячи в воздух, и неровные отклоняются влево либо вправо. Только идеальные сферы летят по прямой линии, и их собирают на другом конце стрельбища.

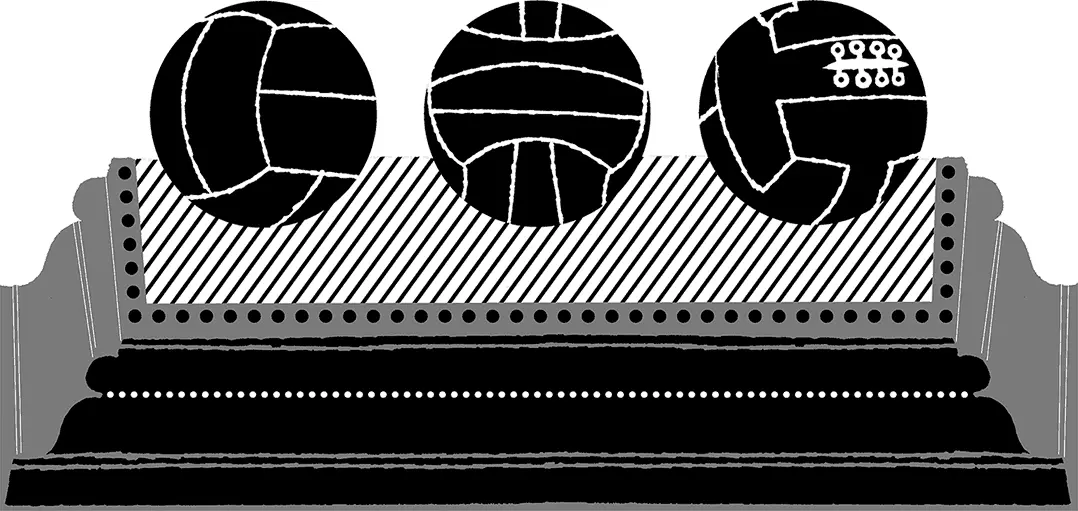
Рис. 2.03. Ранние дизайны футбольных мячей

Как же мы можем сделать совершенную сферу? При подготовке к чемпионату мира по футболу 2006 г. в Германии производители заявляли об изготовлении самого круглого футбольного мяча. Футбольные мячи часто получают путем сшивки нескольких кусков кожи. Многие из футбольных мячей, изготавливавшиеся на протяжении поколений, собираются из форм, которыми играли еще в древние времена. Чтобы узнать, как сделать самый симметричный футбольный мяч, исследуем сначала те «мячи», которые собираются из копий одного симметричного куска кожи. Эти копии расположены таким образом, чтобы у их объединения была симметричная форма, для чего в каждой вершине должно сходиться одинаковое количество граней. Данные формы были исследованы Платоном в диалоге «Тимей», написанном в 360 г. до н. э.