Виктор Лёвин - Вероятность как форма научного мышления

В концепции, развиваемой Мизесом, имеет место также переплетение собственно конструктивных и философских задач, вследствие чего надо различать его теорию частоты и философско-методологическую интерпретацию данной теории. В философском плане эта концепция вписывается в рамки редукционистской программы. Суть последней, как известно, составляют два следующих момента:

1) указание так называемого базисного языка как фрагмента естественного языка;

2) утверждение о том, что познавательная ценность терминов теории определяется их отношением к базисному языку.

Выбор базисного языка дает ряд форм редукционизма, например, феноменализм и физикализм.

Мизесовский подход избирает в качестве базисного языка язык относительных частот. В то же время высказывается убеждение, что возможен перевод в термины относительных частот большинства вероятностных высказываний, используемых в науке.

Исходным пунктом этого подхода является утверждение о тождественности вероятности с эмпирически наблюдаемыми частотами. Поскольку же вероятность выступает как объект математики, требуются средства для перехода от вероятности к эмпирическому материалу. Мизес усматривает это средство в понятии коллектива.

Одно из центральных положений частотной теории звучит: О вероятности можно говорить только в случае, если налицо имеется твердо определенный и отграниченный коллектив. [12] Мизес Р. Вероятность и статистика. М-Л, 1930, с.16. Коллектив, по Мизесу, есть некоторая безграничная последовательность экспериментов, в которой каждый ее элемент (эксперимент) либо наделен, либо не наделен каким-либо определенным признаком (например, таким признаком может быть выпадение фиксированной грани игрального кубика). Причем каждый признак должен иметь в коллективе определенную долю, которая и есть его вероятность.

Важнейшими свойствами коллектива объявляются: существование пределов относительных частот определенных признаков и иррегулярность (Regellosigkeit). Первое свойство совпадает с идеей бесконечности как снятием эмпирических отклонений частот от вероятности. Второе вводится для сохранения собственно вероятностного смысла данной концепции.

Мизес руководствуется соображением, что поскольку вероятность все точнее измеряется при увеличении числа испытаний отношением 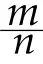(что известно было уже в классической теории из теоремы Бернулли), то в пределе она совпадает с этим отношением. Т. е. Р=lim 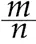, где n → ∞. В традиционном истолковании это соотношение служило выражением лишь одного из свойств вероятности, Мизес же принимает его за определение вероятности.

Доказательство существования пределов относительных частот дается им в чисто эмпирическом плане. Так, он берет пример с бросанием 2-х костей и указывает, что при достаточно большом числе бросаний можно установить постоянство первого десятичного знака в отношении. При дальнейшем увеличении числа бросаний можно установить постоянство дроби, выражающей относительную частоту, скажем, для трех десятичных знаков. Именно этот факт, по Мизесу, должен привести к мысли о сходимости относительных частот, точнее к тому, что предел относительной частоты возможен. [13] Мизес Р. Вероятность и статистика. М-Л, 1930, с. 17–18.

Правило иррегулярности Мизес определял следующим образом: предельное значение относительной частоты, с которым выступает в коллективе какой-либо признак, должно оставаться неизменным, если из всей последовательности произвольно выбрать любую часть и рассматривать в дальнейшем только эту часть. При этом, выбранная частичная последовательность должна быть безграничной, как и сама основная последовательность. То есть, любой признак в любой части коллектива должен иметь ту же самую долю, что и во всем коллективе. [14] Мизес Р. Вероятность и статистика. М-Л, 1930, с.31.

В дискуссии, развернувшейся вокруг понятия коллектива, отмечались трудности как математического, так и принципиального характера. Например, доказывалось, что математика не знает последовательностей, обладающих теми свойствами, которыми наделяет свои коллективы Мизес. В частности, было сказано, что требование предела относительных частот находится в противоречии с требованием правила иррегулярности. Аргументы в этом случае таковы: Понятие предела связано с бесконечной последовательностью, которая не может быть задана актуально вследствие того, что такое задание должно производиться через общий закон образования ее членов по нумерическому признаку. Но это-то и запрещается правилом иррегулярности. В то же время из математики хорошо известно, что только в таком случае можно вести речь о строгом математическом пределе [15] Weismann F. Logische Analyse des Wahrscheinlichkeitsbegrifs. – “Erkenntnis”, I, 1930/31, s.231–232. В другом месте читаем: «…самое понятие предела в его обычном понимании применимо лишь к индивидуальной, закономерно определенной последовательности. Там, где закономерностей, определяющих данную последовательность, нет и принципиально быть не может, нельзя даже ставить вопроса о существовании или несуществовании предела». [16] Хинчин А. Я. Частотная теория Р. Мизеса и современные идеи теории вероятностей. – «Вопросы философии», 1961, № 1, с.79.

Позже Мизес предлагал раскрыть коллектив не как актуальную, а становящуюся последовательность. Но, с математической точки зрения, у такой последовательности также не может быть предела.

В последних своих работах Мизес попытался уточнить определение иррегулярности, объявляя ее уже нечувствительностью не к любому закону выбора, а по отношению к счетному множеству законов, сформулированных в рамках определенной формализованной логики. Ибо, в реальной ситуации речь всегда идет о некотором конечном числе операций выбора. За пределами этой формализованной системы оказывается возможным задать явно случайную последовательность обладающую свойством коллектива, по крайней мере, в принципе. [17] Алешин А. И. и Метлов В. И. Характеристика основных подходов к определению понятия вероятность. – Уч. зап. Горьковского университета. Вып.96. Горький, 1969. На возможность задания случайных последовательностей указывал также А. Г. Постников. [18] Постников А. Г. Арифметическое моделирование случайных процессов. – Труды Мат. ин-та им. В. А. Стеклова, т.57, 1960.

Но главная трудность концепции Мизеса состояла в невозможности на ее основе делать определенные предсказания о течении реальных процессов. И указанное выше уточнение не снимает этой трудности, поскольку не затрагивает понятия предела. Идеализация Мизеса в этом пункте чрезвычайно нечеткая, и ее приложение к реальным испытаниям совершенно не обосновано. Например, согласно позиции Мизеса, мы не можем сказать хотя бы предположительно заранее, сколько раз при 1000 подбрасываний «правильной» монеты выпадет «герб». По Мизесу надо бы ответить, что возможны все числа – от 0 до 1000 раз. Реальное же испытание дает некоторое устойчивое число, вокруг которого группируются выпадения «герба». Без дополнительного постулата, как указывал А. Я. Хинчин, до произведения испытаний Мизес не может сделать никакого выбора из возможных чисел выпадения «герба». Можно лишь вычислить вероятность того, что «герб» выпадет столько-то раз. [19] Хинчин А. Я. Учение Мизеса о вероятностях принципы физической статистики. УФН, 1929, вып.2, с.153.