Джордан Элленберг - Как не ошибаться. Сила математического мышления

Вот как это работает. Вы хотите установить взаимозависимость между двумя параметрами, скажем между стоимостью обучения в университете и средним баллом по отборочному тесту SAT принятых на учебу студентов. Возможно, вы считаете: чем выше средний балл SAT, тем дороже учебное заведение, – но посмотрите на данные, которые говорят, что это далеко не универсальный закон. В Университете Элона, расположенном на окраинах Берлингтона (штат Северная Каролина), средний совокупный результат по математике и английскому языку составляет 1217 баллов; при этом университет взимает плату за обучение в размере 20 441 доллара в год. Обучение в Колледже Гилфорда, расположенном рядом, в городе Гринсборо, обходится немного дороже – 23 420 долларов, но средний результат первокурсников по SAT составляет там всего 1131 балл.

Вместе с тем, если вы посмотрите на весь список учебных заведений Северной Каролины – тридцать один частный университет, данные об оплате за обучение и о среднем балле которых были представлены в 2007 году в «Сети ресурсов для построения карьеры штата Северная Каролина», – вы увидите четкую тенденцию {31}.

На представленном ниже рисунке каждая точка графика соответствует одному из колледжей. Вы видите те две точки, которые находятся в правом верхнем углу, с высоким средним баллом SAT и столь же высокой платой за обучение? Это Университет Уэйк Форест и Университет Дэвидсона. Одинокая точка в нижней части рисунка соответствует единственному частному учебному заведению в этом списке, плата за обучение в котором меньше 10 тысяч долларов, – Колледжу медицинских наук Кабаррус.

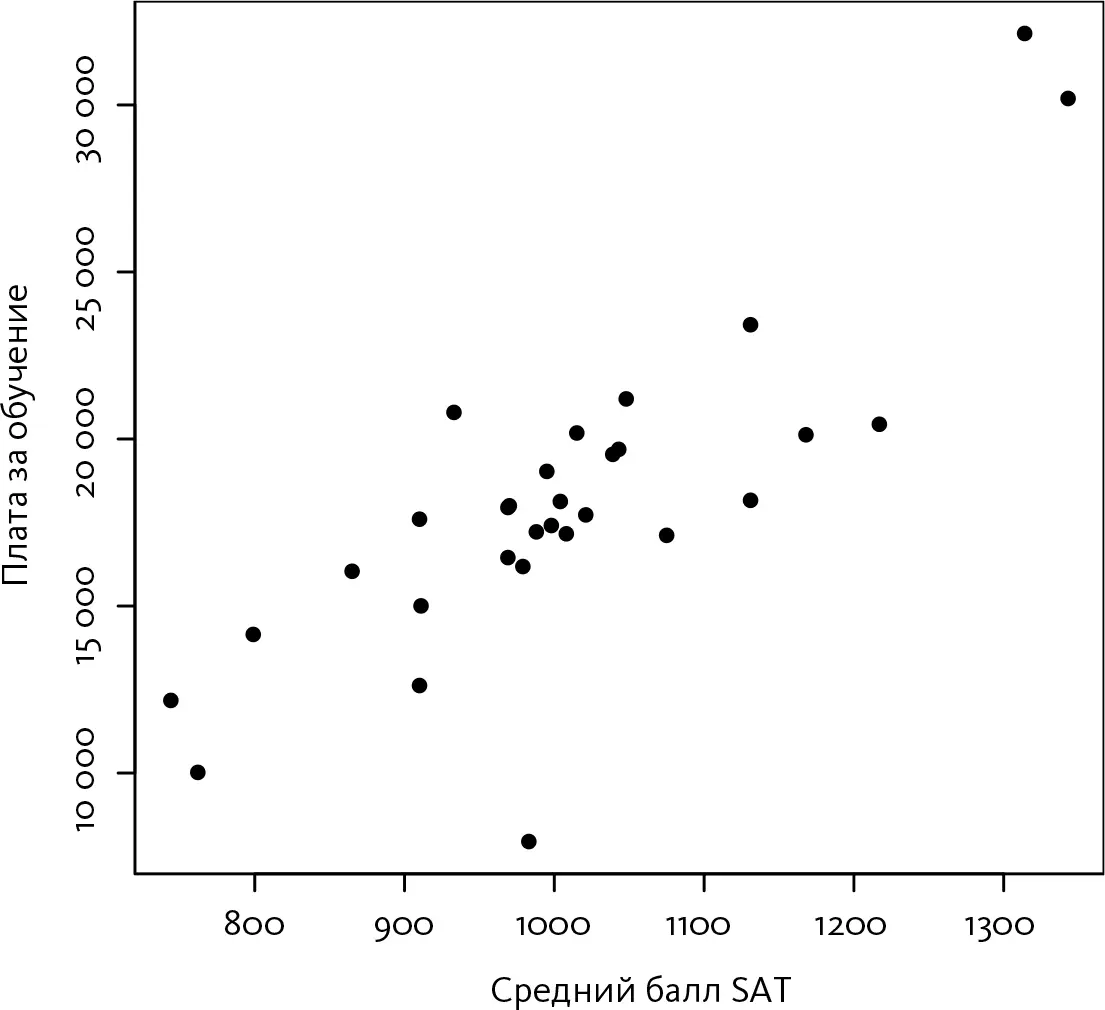
Данный рисунок четко показывает, что в учебных заведениях с более высоким средним баллом SAT цена за обучение, как правило, выше. Но насколько выше? Именно здесь на сцену выходит линейная регрессия. Очевидно, что точки на рисунке не образуют прямую линию, но видно, что они находятся не так уж далеко от прямой. Пожалуй, можно было бы вручную нарисовать прямую линию, проходящую посередине этого облака точек. Линейная регрессия исключает угадывание и позволяет найти прямую линию, максимально приближенную ко всем точкам [55]. В случае университетов штата Северная Каролина эта прямая выглядит так, как на следующем рисунке.

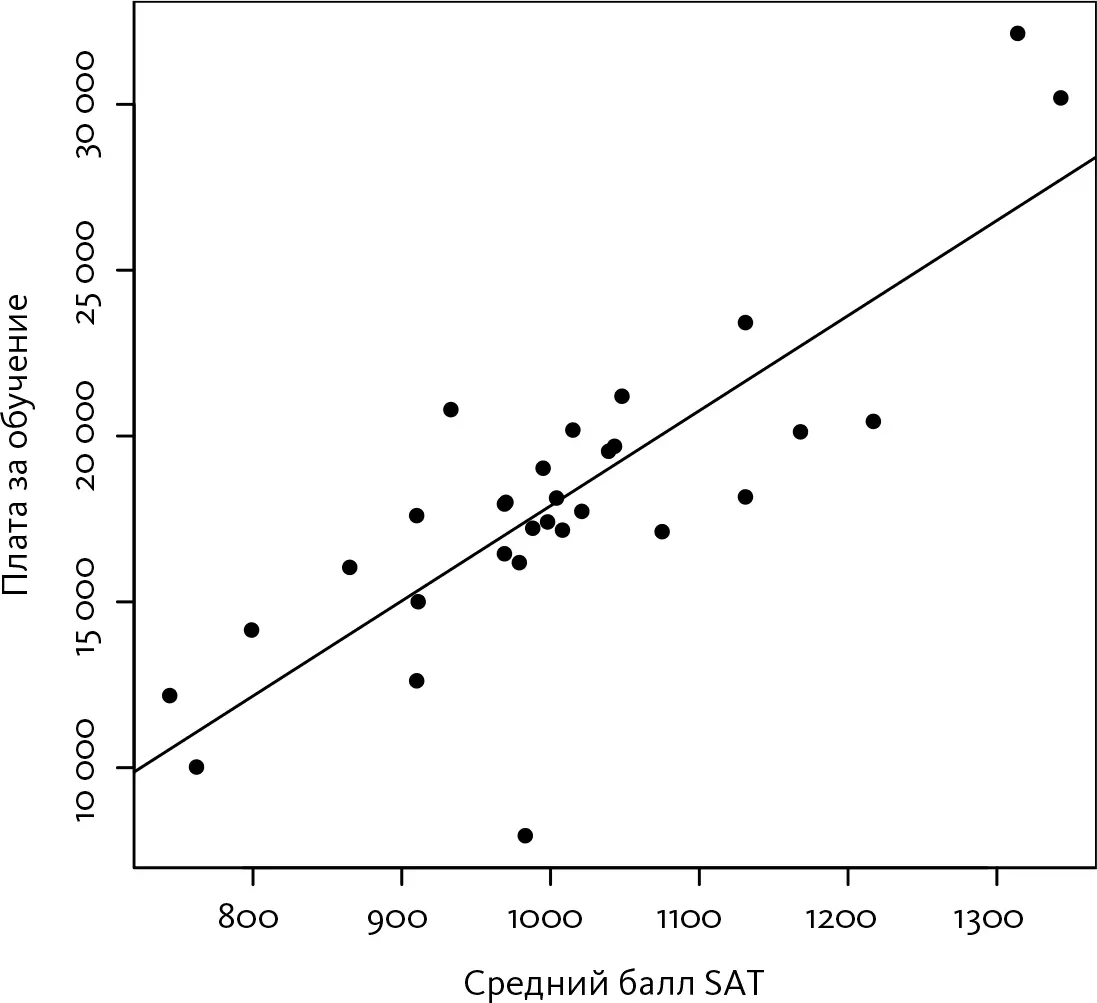
Коэффициент наклона изображенной на рисунке прямой равен 28. Это означает следующее: если плата за обучение зависела бы только от баллов SAT, которые задает прямая на графике, тогда на каждый балл SAT приходилось бы дополнительных 28 долларов платы за обучение. Если вам удалось бы поднять средний балл первокурсников на 50 пунктов, тогда вы могли бы назначить более высокую плату за обучение – на 1400 долларов. (Или, с точки зрения родителей, если ваш ребенок на 100 баллов улучшит свой результат отборочного теста, это обойдется вам в дополнительных 2800 долларов в год. Курс по подготовке к тесту оказался более дорогим, чем вы думали!)

Линейная регрессия представляет собой замечательный инструмент: гибкий, масштабируемый и легкий в применении (вы просто нажимаете соответствующую кнопку электронной таблицы). Этот инструмент можно применять к двум наборам данных с участием двух переменных, как в приведенном выше примере, но он работает не менее эффективно и в случае трех или даже тысячи переменных. Каждый раз, когда вам нужно понять, как одни переменные меняют другие переменные и в каком направлении, линейная регрессия – это первое, что следует использовать. Этот инструмент применим буквально к любому набору данных.

Однако в этом заключается не только сильная, но и слабая сторона линейной регрессии. Вы можете применить этот метод, не задумываясь, действительно ли феномен, который вы пытаетесь моделировать, близок к линейному. Но вы не должны так делать . Я сказал, что линейная регрессия подобна отвертке – что действительно так; однако в другом смысле она скорее напоминает циркулярную пилу. Если вы примените этот инструмент без тщательного анализа того, что вы делаете, результаты могут оказаться плачевными.

Возьмем в качестве примера ракету, которую мы с вами запустили в предыдущей главе. Возможно, вы не имеете никакого отношения к ее запуску. А может быть, напротив, представляете собой ту цель, на которую эта ракета направлена. В последнем случае вы особенно заинтересованы в как можно более точном анализе траектории движения ракеты.

Вы могли бы нанести на график положение ракеты по вертикали в пяти точках по времени. Такой график выглядит следующим образом.

Теперь вы в состоянии быстро выполнить линейную регрессию, получив замечательный результат: линию, которая проходит почти через все точки на графике.

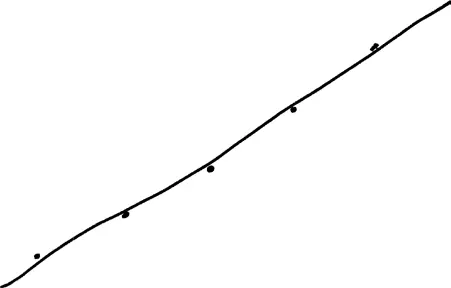
(В этот момент ваша рука начинает приближаться к острому полотнищу циркулярной пилы.)

Построенная вами линия представляет собой весьма точную модель движения ракеты: за каждую минуту ракета поднимается вверх на определенное фиксированное расстояние, скажем на 400 метров. Через час ракета окажется в 24 километрах над поверхностью земли. Когда же она опустится на поверхность? Никогда! Направленная вверх наклонная прямая линия по-прежнему стремится вверх. Именно так ведут себя прямые.

(Кровь, травмы, вопли.)

Однако не каждая линия является прямой. А траектория полета ракеты несомненно представляет собой не прямую, а параболу. Подобно окружности Архимеда, вблизи она действительно похожа на прямую, поэтому линейная регрессия сослужит вам большую службу, позволив определить местоположение ракеты через пять секунд после запуска. Но через час? Даже не думайте об этом. Ваша модель говорит о том, что через час ракета находится в нижних слоях стратосферы, хотя на самом деле она, возможно, уже приближается к вашему дому.

Возможно, самое образное предостережение в отношении бездумной линейной экстраполяции сформулировал не статистик, а Марк Твен в романе Life on the Mississippi («Жизнь на Миссисипи»):

…Длина Миссисипи между Каиром и Новым Орлеаном сто семьдесят шесть лет тому назад была тысяча двести пятнадцать миль. После прорыва русла в 1722 году длина стала тысяча сто восемьдесят миль. Когда образовался рукав у Американской излучины, длина стала тысяча сорок миль. С тех пор этот участок реки укоротился еще на шестьдесят семь миль. Следовательно, сейчас ее длина между Каиром и Новым Орлеаном всего девятьсот семьдесят три мили.